1 Computing on Functions Using Randomized Vector Representations (in brief
2 Computing on Functions Using Randomized Vector Representations 33页版本
https://arxiv.org/abs/2109.03429
向量的加法对应于函数的加法,向量的绑定对应于函数的卷积。
我们设想 VFA 框架将有助于构建⼀种⼈⼯智能,它使⽤分布式、可解释的表⽰,并且可以通过具有明确定义的计算意义的代 量运算进⾏处理。这种⼈⼯智能⽅法可以结合神经⽹络、概率推理和符号⼈⼯智能的优点;也就是说,学习的能⼒,在分布式硬件上可 执⾏的能⼒,以及具有基于规则的推理能⼒来概括和推断先验知识的能⼒。我们相信该⽅法还可能有助于深⼊了解⼤脑中⾼度分布 的表征,例如内嗅⽪层和海⻢体。
将KLPE和VSA相结合,产生了一个我们称之为向量函数架构(VFA)的计算框架
VFA的先决条件是与VSA绑定操作兼容的KLPE。我们现在关注一种特定的LPE,分数幂编码(FPE)

后续论文:
脑启发全息自适应编码器的超维计算
一个超强学习算法及5大特点

摘要:
用于通过随机向量对符号进行编码的符号处理的向量空间模型已经在认知科学和联结主义社区中被提出, 名 称为向量符号架构(VSA), 同义地为超维(HD) 计算[22,31,46 ] 。在本文中, 我们通过将连续值数据映射到向量空间中, 将 VSA 推广到函数空间, 使得任意两个数据点表示之间的内积近似表示相似核。类比VSA, 我们将这种新的函数编码和计算框架称为向量函数架构(VFA)。在VFA中, 向量可以表示各个数据点以及函数空间(再现内核希尔伯特空间) 的元素。从VSA继承的代数向量运算对应于函数空间中明确定义的运算。此外, 我们研究了先前提出的一种用于编码连续数据的方法, 即分数幂编码(FPE), 该方法使用随机基向量的求幂来生成数据点的随机表示, 并满足诱导 VFA 的内核属性。我们表明, 对基向量的分量进行采样的分布决定了 FPE 内核的形状, 这反过来又引 发了用于使用带限函数进行计算的 VFA。特别是, VFA 提供了一个代数框架, 用于实现具有随机特征的大规模内核机器, 扩展了[51]。最后, 我们演示了 VFA 模型在图像识别、 密度估计和非线性回归问题中的几种应用。
我们的分析和结果表明,VFA 构成了⼀ 个强⼤的新框架,⽤于表⽰和操纵分布式神经系统中的功能,在⼈⼯智能中具有⽆数的应⽤。
8 讨论
8.1 结果总结
我们的主要贡献是对向量函数架构(VFA)进行了正式的描述,这是一种通过操作高维随机向量来计算函数的新框架。这项工作推广了向量符号架构(VSA)模型用于符号推理,并且它还正式化了一些早期使用VSA处理亚符号数据的建议(见下文8.4.1节)。我们的结果可以归纳为以下陈述:
• 结合与VSA绑定操作兼容的KLPE可以产生向量函数架构(VFA),即在其中函数由向量表示,并且可以通过形成表示空间上代数的向量操作来操作的再生核希尔伯特空间(RKHS)。代数量子操作可以执行以下函数操作:点评估、积分、加法、平移和卷积(定理1)。
• 在VSA中,两个符号表示的向量绑定形成一个符号对的表示,表达符号之间例如键值或角色填充者的关联。有趣的是,在VSA框架中,函数向量的绑定表达函数卷积。卷积已被证明是函数的重要组合/分解操作,正如卷积神经网络(Bengio等人,2021)的成功所示范。
• 基于VSA绑定操作的分数幂编码(FPE),一种现有的LPE方法,为一维和多维数据空间诱导VFAs。核形状取决于FPE基向量的随机结构。均匀采样的基向量产生具有通用核形状的VFAs,即sinc函数,与底层绑定操作无关。因此,结果VFA中的向量可以表示带限函数(定理2)。
• 描述了如何在VFA中塑造核的方法。具体来说,任何具有在[-1/2, 1/2]内带限的傅里叶密度的核都可以通过相应地采样FPE基向量在VFA中产生。特别地,展示了如何构建对各种应用有用的VFE核,例如高斯核、非笛卡尔多维sinc核、周期性网格核等。
• 像传统的符号VSAs一样,VFAs需要一种检测、解码和去噪表示的机制。提出了一种电路机制来实现这一目的。
• 展示了一些使用VFA进行核计算的例子,图像处理、密度估计和非线性回归。
• 其他类型的LPEs(过去曾与VSA一起使用),如浮点编码、随机向量连接和随机投影,也可以诱导RKHS函数空间。然而,这些其他的LPEs没有一种能诱导VFA,因为它们不包括与编码方案兼容的绑定操作,见补充材料C。
8.2 VFA的技术应用
除了由下面8.4.1节中的早期相关工作开创的VFA应用之外,这里提供的函数空间和代数函数运算的精确定义为许多新颖的应用铺平了道路。它们包括:
•VSAs/超维计算:VFA提供了一个代数的,理论上的方法来扩展VSAs超维计算技术到函数计算。有关应用示例,请参见第7.1节。
•大规模内核机器:VFA为大规模实现内核方法提供了特征表示和向量运算。通过将核表示为特征向量的内积来克服传统核方法(Bach,2019)的维数灾难的想法已经在(Rahimi和Recht,2007)中指出,参见第8.4.2节。有关VFAs内核应用的示例,请参见第7.2节。
•概率数据结构/草图:概率数据结构或草图是由数据点形成的数学对象的简化表示(Mitzenmacher和Upfal,2017)。这种简化的表示比存储所有单个数据点在计算和存储方面更高效。本质上,VFA向量可以被视为一个紧凑的概率数据结构或一个函数(7.2节)或一个对象(7.1节)的草图。有趣的是,vfa给概率数据结构增加了新的功能。具体来说,单个VFA向量可以实现内核机器的功能,超出了草图的标准应用领域,如成员测试(布鲁姆过滤器(布鲁姆,1970))或频率估计(计数-最小草图(Cormode和Muthukr- ishnan,2005))–例如,参见第7.2节。
•储层计算:之前已经强调过,储层计算可以在递归网络中实现VSAs的代数框架(Frady等人,2018cKleyko等人,2020a)。将输入编码从常规储层计算中的随机投影方法改变为KLPEs将产生一类新的递归网络,用于在明确定义的函数空间中以透明的方式进行计算。
•神经网络:据推测,神经网络中绑定操作的缺失是其缺乏数据效率、泛化和鲁棒性的根源(Greff等人,2020)。通过VFAs将VSA绑定概念从符号域推广到函数域是开发具有绑定操作的神经网络方法的关键步骤。此外,通过将函数表示为向量,VFA为电流型神经网络处理函数提供了一个有趣的输入接口。此外,内核和深度学习之间存在已知的联系,具体而言,基于梯度的学习可以根据所谓的路径内核(Domingos,2020),神经切线内核的扩展(Jacot等人,2018)来制定。这种核是否可以用VFAs表示,是未来研究的一个开放问题。
•动态认知建模:为了对大脑的认知功能进行建模,已经提出了例如(Port和Van Gelder,1995;Eliasmith,1996),将离散符号推理映射到连续动力系统,特别是动态神经场模型(Amari,1977;厄门特劳特和麦克劳德,1993年;吉尔萨和哈肯,1996年;Erlhagen和Sch oner,2002)。这些模型引入了一个连续的低维拓扑空间作为内部或“精神”导航空间。已经强调了向量符号概念如何能够构建动态认知模型,但是挑战性的逆问题仍然存在,即如何适当地设计精神空间和适合解决给定认知问题的神经动力学(Beim Graben和Potthast,2009;Widdows和Cohen,2015)。使用VFA能够在心理空间中形成相似性结构,这可能为解决具有挑战性的认知任务的逆问题提供新的方法。
8.3 神经科学的VFA模型
VFA作为大脑中神经元编码模型的预测关键取决于编码/结合方法的选择。经典VSA的结合操作,Hadamard乘积和循环卷积,不容易映射到生物神经元回路的功能上。它们还需要密集的表示向量,这似乎与神经记录中稀疏活动模式的观察不相容(Rachkovskij和Kussul,2001;弗雷迪等人,2021年)。然而,有趣的是,Hadamard FPE中使用的相量矢量可以自然地用尖峰来表示,其中复相位由周期性尖峰模式的定时来表示(Frady和Sommer,2019)。人们可以在相量码中引入群体稀疏性,并为神经元子集中具有模拟相位角的模式构建高容量联想记忆网络(Frady和Sommer,2019)。块局部循环卷积(第4.2.3节)是一种可以用这种代码操作的绑定操作。潜在地,这种结合方法可以通过生物学机制实现(Frady等人,2021),例如,利用活性树突和符合检测(Schaefer等人,2003)。
以前曾尝试使用Fractional Power Encoding (FPE)建立海马/内皮层的模型。具有尖峰定时相位码的这些模型之一展示了与实验观察一致的现象,
例如位置场和相位进动(Frady等人,2018a)。另一个基于速率编码和循环卷积结合的模型(Komer和Eliasmith,2020)表明,模型神经元可以表现出网格细胞样的响应。推测海马和内嗅皮层是否能够实现和利用全部VFA功能是很有趣的。海马/内嗅皮层的VFA模型将预测活动模式可以代表环境空间的功能,如奖励和未来路径的概率密度。尽管基于速率的模型实现了完整的VFA,但是在最初的出版物中没有利用表示函数的能力。相位编码海马体模型(Frady等人,2018a)可通过添加绑定操作(如第4.2.3节所述的块局部循环卷积)扩展至全VFA。
VFA揭示了神经编码的潜在计算作用。神经编码通常被视为对感觉信号的内在结构进行统计学习的结果。例如,信源编码(Shannon,1949年)或冗余减少(Barlow,2001年)的目标通常可以导致维数减少,但当与稀疏性结合时,也会导致维数增加(Olshausen和Field,1996年)。神经编码的其他理论是基于随机抽样,而不是学习,例如,使用随机突触投射。此类模型的计算目标包括哈希运算,以形成扩展的地址空间,从而改善信号检测(Babadi和Sompolinsky,2014年;Fusi等人,2016;达斯古普塔等人,2017),或压缩感知(多诺霍,2006;Cand`es等人,2006),用于优化布线约束下的神经通信(Isely等人,2010;希拉和索默,2015;Ganguli和Sompolinsky,2012年)。
VFA调和了基于学习和基于随机的神经编码理论。
一个VFA理论做出如下预测:
a)有意义的低维感觉信号流形被提取出来(这里不讨论),然后通过高维随机活动模式重新编码。高维表示空间中的内积近似于数据流形上的相似性核。
b)高维向量空间可以表示和操纵数据流形上的点和函数。点和可用函数空间之间的相似性由核决定。
c)学习是核函数空间中的近似。
d)向量之间的绑定使得能够通过卷积从已经学习的函数原语合成新函数。
e)神经相关性和“信号混合”的作用,如前面模糊定义的,可以变得明确:群体活动中的相关性编码信息,该信息可以通过将群体活动向量与记忆向量进行比较来解码。信号可以以不同的方式混合,通过绑定保持相似性,或者通过绑定破坏相似性。
脑功能的大部分计算理论,如贝叶斯推理、预测编码等。,需要神经元群体活动的功能编码。可能最接近VFA概念的是总体编码(Pouget等人,2000年;Barber等,2003),如贝叶斯总体码(马等,2006)。在这些模型中,每个神经元通常在编码流形上有一个高斯形状的感受野。这导致内积核随距离衰减并且是平移不变的。因此,贝叶斯总体代码诱导核函数空间。然而,它们缺乏绑定操作(至少我们不知道)来执行VFA可能的代数函数操作。
1 简介:
⼈⼯智能 (AI) 领域近期令⼈印象深刻的成就是由计算嵌⼊⾼维向量空间中的数据表⽰的模型驱动的,迄今为⽌最引⼈注⽬的是神 经⽹络(Bengio 等⼈,2021)。⼀旦提供了输⼊数据和监控信号(如果适⽤),神经⽹络就会提供强⼤的端到端训练机制来优化 给定任务的性能。然⽽,最先进的神经⽹络仍然⾯临两个基本问题。⼀是所学知识的应⽤很脆弱,并且不容易推⼴到训练集之外的新环境。有⼈认为,这个问题部分是由于⽆法进⾏变量绑定(Fodor 和 Pylyshyn,1988;Greff 等⼈,2020),这对于使在⼀个领域 学到的知识能够分离并灵活地应⽤于其他领域⾄关重要(Smolensky,1990)。当前神经⽹络的第⼆个固有问题是缺 乏透明度。也就是说,神经⽹络中的向量表⽰和变换在计算⽅⾯都没有明确的解释。尽管通过加权和和阈值组合信号的显式计算对 于⽹络中的每个神经元都得到了很好的指定和理解,但整个系统通常被视为⿊匣⼦,⽽没有深⼊了解所学习的表⽰的数学结构或底层计算由整个⽹络执⾏的功能。缺乏透明度是使⽤神经⽹络作为⼤脑功能解释模型以及分析、理解或解释神经⽹络在特定应⽤环 境中的决策的障碍。
近年来,我们和其他⼈在推进称为⽮量符号架构 (VSA) 或同义超维 (HD) 计算的⽮量空间计算框架⽅⾯取得了进展,该框架既 ⽀持变量绑定⼜完全透明(Plate,1994a;Kanerva,1996) ;盖勒,1998a;Eliasmith 和 Thagard,2001;Rachkovskij 和 Kussul,2001)。在 VSA 中,符号、数据或其他实体通过将它们随机映射到固定维度的向量空间来表⽰。这些向量的代数由加法、乘 法和排列组成,分别实现了捆绑、结合和排序操作(Kleyko 等⼈,2021)。现在,这种⽅法有多个成功的例⼦应⽤于⽂本分析 (Jones and Mewhort,2007;Joshi 等,2016a;Recchia 等,2015)、EEG 和 EMG 信号解码(Rahimi 等,2019;Moin)等⼈, 2021)、序列学习(Hannagan 等⼈,2011;Frady 等⼈,2018c)和机器⼈技术(Neubert 等⼈,2019)。然⽽,迄今为⽌,⼤多数 这些应⽤程序仅限于离散数据,例如⽂本、单词或其他标记,或者通过离散化本质上基本连续的数据,从⽽忽略数据中重要的拓扑相似关系(Edelman,1998)。
在本⽂中,我们讨论如何在向量空间中表⽰连续数据和函数,以及如何通过 VSA 代数来操作它们的问题。我们开发了⼀种新的向 量空间函数计算框架,与 VSA 类⽐,我们将其称为向量函数架构 (VFA)。与 VSA ⼀样,VFA 是完全透明的。向量可以表⽰各个数据点 以及被明确定义为再现核希尔伯特空间的函数空间的元素。函数的域可以对数据中的连续值量进⾏编码,例如位置、时间或波⻓。函数通过 VSA 的向量运算进⾏操作:向量的加法对应于函数的加法,向量的绑定对应于函数的卷积。函数域通过对固定随机基向量取幂 进⾏编码这种编码之前已作为分数幂编码引⼊,这些编码和操作共同打开了⼀种强⼤的新数据计算⽅式的⼤⻔,例如图像、声⾳波形和⽆数其他类型的连续信息流,⼈们希望在这些 数据流中操纵函数(就像⽬前在符号计算中所做的那样)。
除了与 VSA 的关系之外,VFA 还可以被视为更⼤类算法的⼀部分,这些算法利⽤随机性来扩展维度,例如散列(Cormen 等 2009 年;Dasgupta 等⼈,2008 年)、随机计算(Alaghi 和Hayes,2018)、储层计算(Frady 等⼈,2018c;Cuchiero 等⼈,202 或降维例如压缩感知(Cand`es 等⼈,2006;Donoho,2006;Frady 等⼈, 2021)。特别是,VFA 提供了⼀个代数框架,⽤于 实现具有随机特征的⼤规模内核机器,包括和扩展 Rahimi 和 Recht (2007)。另⼀⽅⾯,VFA 与所有这些⽅法的区别在于,它包含⼀ 个基于数学的框架,⽤于计算高纬表示。
我们设想 VFA 框架将有助于构建⼀种⼈⼯智能,它使⽤分布式、可解释的表⽰,并且可以通过具有明确定义的计算意义的代 量运算进⾏处理。这种⼈⼯智能⽅法可以结合神经⽹络、概率推理和符号⼈⼯智能的优点;也就是说,学习的能⼒,在分布式硬件上可 执⾏的能⼒,以及具有基于规则的推理能⼒来概括和推断先验知识的能⼒。我们相信该⽅法还可能有助于深⼊了解⼤脑中⾼度分布 的表征,例如内嗅⽪层和海⻢体。
本文其余部分的组织如下。第2节回顾了经典的VSA模型,并陈述了功能分析的结果,这些结果对本文至关重要。在第3节中,我们用内积核重新表述符号VSA,并将这些核推广以描述通过局部保持编码(LPE)映射到向量的实值数据的相似性。在一定条件下,得到的向量空间模型表现出透明性,并形成VFA,即向量代表定义函数空间中的函数,VSA向量运算在函数空间中执行特定运算。第4节描述了使用称为分数幂编码或分数绑定(Plate,1992,1994b)的现有LPE方法构建VFA。我们将分数幂编码推广以产生具有相量值、实值和稀疏表示的VFAs,以及可以高效地在硬件中实现的代数运算。在第5节中,我们分析了VFA中可能的核形状。值得注意的是,通过在FPE中非均匀采样基向量,可以轻松构建具有各种不同应用的VFA的核。在第6节中,我们描述了如何在VFA中解码和去噪给定的向量。解码提供了VFA计算的透明性。去噪,类似于VSA,对于防止来自模拟计算机的误差积累至关重要。在第7节中,我们展示了VFAs的应用。最后,第8节的讨论总结了我们的结果,并解释了对技术应用和神经科学的影响,以及与先前文献的关系。
2 背景
2.1 符号VSA模型
如何在高维向量空间中表示和处理信息的问题不仅在认知神经科学(Gayler,2003;Günther等人,2019)有着悠久的传统,而且在语言处理(Van Rijsbergen,2004;Widdows,2004)中也是如此。这里,我们的出发点是用于符号认知推理的向量模型,称为向量符号体系结构(VSA)或超维计算(Plate,1995;Kanerva,1997;Gayler,1998a;Rachkovskij,2001)。
VSA是具有向量表示的符号推理模型,具有两个区别属性。第一个是符号由随机的n维向量表示。在经典的VSA模型中,符号由其分量从指定分布中独立同分布抽取的向量编码。这种编码策略确保了不同符号的表示是良好分离的,其中符号的相似性通常通过向量之间的内积来衡量,或者内积的简单函数,如余弦相似性。在这里,我们通常使用带有模型依赖的归一化因子的内积来表示相似性。为了书写简便,以下将省略归一化因子。在VSA中,通过将向量与存储在码本中的符号表示向量进行比较来解码向量。解码和基于记忆的去噪是VSA计算过程中的一个重要步骤,因为它防止了模拟计算中有害的误差积累(Marsocci,1956)。
不同的VSA模型使用不同类型的随机向量。例如,二进制散斑码使用二进制向量(Kanerva,1997),全息缩减表示使用实值向量(Plate,1995),频率域全息缩减表示使用复值向量(Plate,1995)。大多数VSA模型不支持稀疏表示(但请参见Rachkovskij(2001)),在能量消耗和突触记忆使用方面,稀疏表示具有优势。最近,有人提出了使用具有块结构的稀疏向量的VSA模型(Laiho等人,2015;Frady等人,2021),这与模块化复合表示VSA模型(Snaider和Franklin,2014)有关。
VSA的第二个基本属性是,所有计算都可以通过少量的基本向量运算来组合,这些运算连同向量表示空间一起形成一个代数环结构。VSA至少具有两个基本的二元运算,它们将两个(或两个以上,通过连续执行)向量映射到一个新的向量。捆绑操作:

通常用于表示符号集合(Kleyko等人,2020c),并简单地是相应符号向量的分量和(叠加)。可以通过在集合表示和单个符号表示之间形成内积来读取由s表示的集合的元素。根据向量维度,可以通过高内积精确检测集合的元素;关于这种“读出”的理论分析,请参见Frady等人(2018c);Thomas等人(2020);Kleyko等人(2020d)。
相反,绑定操作:

通常用来表示两个向量之间的关联,如键值对(Kanerva, 2009)。
绑定的一个重要属性是存在逆操作,即解绑,它从由(2)形成的复合数据结构z中提取出其一个成分:



这里的
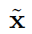
表示 x 在绑定方面的逆。存在一些自然组合的随机向量类型和特定的绑定操作,即那些绑定操作保持向量类型的组合。例如,对于双极(Kanerva, 2009)或相位向量(Frady et al., 2018c),哈达玛德积保持了向量类型,而对于二进制向量(Kanerva, 1997)则是逐位 XOR 操作。对于实数或复数值的随机向量(Plate, 1995),圆周卷积保持了向量类型,对于块稀疏向量,则块局部圆周卷积(Frady et al., 2021)做到了这一点。
二元向量操作和符号表示的结合使得 VSA(向量空间代数)模型能够表示和查询一系列令人印象深刻的数据结构(见 Kleyko et al. (2021) 的概述),例如键值对(Kanerva, 2009)、集合(Kleyko et al., 2020c)、直方图(Joshi et al., 2016b)、序列(Hannagan et al., 2011)、树(Rachkovskij 和 Kussul, 2001; Frady et al., 2020)、栈(Yerxa et al., 2018)、状态自动机(Osipov et al., 2017)等。
VSA 已经通过将符号和代数特性与局部性保持编码(LPE)方法相结合来扩展处理实数值数据,这些方法在应用中显示出了前景(Plate, 1992; Weiss et al., 2016; Rahimi et al., 2017; Frady et al., 2018b; Komer et al., 2019),但之前缺乏理论基础。为了提供坚实的理论基础,我们基于函数分析的基本结果,这些结果在下一节中描述。
2.2 将VSA扩展到实数值数据的泛函分析结果
为了处理连续流形上的数据,VSA已经与局部性保持编码(LPE)方法相结合(Plate, 1992; Weiss et al., 2016)。在第3.1节中,我们将展示符号VSA中的编码如何以内积相似性核的形式表述。在第3.2节中,我们推广了符号VSA的内积相似性核来描述LPE。在本文中,我们将重点关注核局部性保持编码(KLPE),即具有平移不变性、正定性、平滑衰减相似性核的LPE(见第3.2节中的定义)。将KLPE和VSA相结合,产生了一个我们称之为向量函数架构(VFA)的计算框架,在其中不仅符号,而且实数值数据和函数可以以透明的方式被表示和操作。下面的泛函分析的定义和结果对于理解VFA中所代表的对象至关重要。
定义:如果对于任意有限点集{x1, x2, ..., xm},文法矩阵K(xi, xj)是正定的(即,所有特征值都是非负的),则核K(x1, x2)是正定的。
定理:所有内积核都是正定的(Schöolkopf et al., 2002; Hofmann et al., 2008)。
我们的第一个中心结果,定理1,VFA中表示和操作的数学解释,将利用Nachman Aronszajn(1907-1980)的以下定理。
定理(Aronszajn, 1950):每个正定核定义了一个再生核希尔伯特空间(RKHS)。

以下著名的Salomon Bochner(1899-1982)定理将被用来分析VFAs并设计具有所需相似性核形状的模型。
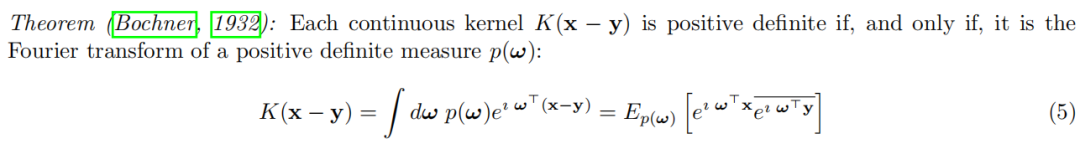
证明:关于这个定理的表述和证明,请参见Rudin(1962年)。
核方法最初由Aizerman等人(1964年)在非线性模式识别中使用,并在1990年代成为机器学习的一个基石。关于核方法的泛函分析以及其在机器学习中应用的优秀教科书,见Schöolkopf等人(2002年)。
3 向量函数架构(VFA)
在这一部分,我们定义并描述了VSA的一种概括,用于计算函数,它与第2.1节中描述的原始符号VSA共享其透明度。我们对VSA的概括从重新制定符号VSA开始,以下面小节中描述的内积相似性核的形式表述。
3.1 符号VSA的核

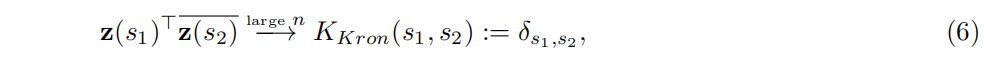

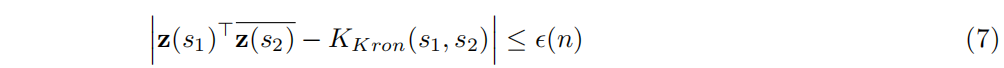

在VSA计算中,这些误差的校正以及其他来源的噪声是一个重要部分——它防止了不可控制的误差累积,这是模拟计算机的一个主要问题(Marsocci, 1956)。在VSA中进行误差校正时,出现在输入中或在代数推理过程中的向量与分配给符号的基础向量进行比较。在符号VSA中,通常通过内容寻址存储器完成检测和去噪(Plate, 1995; Gritsenko et al., 2017)。检测过程的正确性取决于噪声量,并且可以通过信号检测理论来预测(Frady et al., 2018c)。
3.2 保持局部性的核编码
典型的VSA表示使用独立随机向量仅通过内积编码二元信息,即“相同”与“不同”,关于编码对象之间关系的。要在对象之间编码等级相似性信息,需要一种专门的局部性保持编码(LPE)方法。LPE为流形上的点产生向量表示,以便向量的内积反映了点之间的关系。这允许数据在数据流形的上下文中被表达和操作。

其中,核函数K(d)是实值的,在d = 0处达到最大值,并逐渐在|d|较大时达到零。在相当普遍的条件下,(8)中的收敛是快速的:
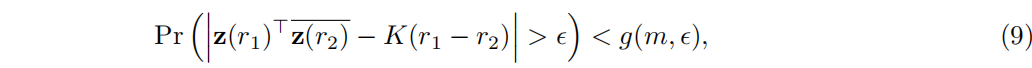

3.3 VFA 的定义和属性
基于第2.2节中提到的Aronszajn定理(1950年),我们可以简洁地定义VSA和KLPE的结合并描述其属性。我们从以下定义开始:
定义2:KLPE与VSA绑定操作 ∘∘ 兼容,如果编码变量的两个值的加法可以通过绑定值的个别表示来表示:

函数的逐点加法(14)来源于内积核的线性。
函数平移(15)来源于RKHS的性质,见VFA定义,以及KLPE与绑定(10)的兼容性。
函数卷积(16)可以计算为:

4 VFA与分数幂编码(FPE)
前一节定义并描述了VFA的一般情况。VFA的先决条件是与VSA绑定操作兼容的KLPE。我们现在关注一种特定的LPE,分数幂编码(FPE),它基于绑定操作,并在早期的VSA文献中已经介绍过(Plate,1994a)。我们描述了FPE的不同形式,展示了它们是与绑定兼容的KLPE。这些发现表明,将VSA与FPE结合的早期模型确实符合VFA的标准 - 尽管它们表示和操作函数的能力并没有被明确地利用。
4.1 Plate分数幂向量的概括
FPE是分数幂向量(Plate,1992, 1994a)的概括,这是一种基于圆周卷积绑定的拓扑空间编码的LPE方法。这里我们将概念概括到其他VSA绑定操作。FPE从自绑定开始,即绑定一个基向量,一个随机向量 \( z \sim p(z) \),自乘 i 次,这为整数定义了一个编码策略:


4.2 现有的绑定操作导致不同类型的VFA
FPE 关键依赖于 VSA 绑定操作,图 1 所示向量集的属性取决于单个绑定操作。接下来,我们基于先前提出的绑定操作(哈达玛积、循环卷积或局部块循环卷积)定义并分析 FPE 的属性。对于相应的 VFA,这些定义产生了用于计算定理 1 中的函数操作以及图 1 所示集合的具体公式。
4.2.1 基于Hadamard乘积的VFA
两个向量之间的Hadamard乘积是向量分量相乘得到的向量:

这种关系将在下文中用于确定哈达玛 FPE 的核形状。哈达玛 FPE 需要一个复杂的状态空间。一个常用的 VSA 框架 (Gayler, 1998b; Kanerva, 2009) 使用具有哈达玛积绑定的实值分量,其中保持范数的向量是双极性向量。然而,不能基于哈达玛积定义形成实值向量的 FPE。首先,r 的所有偶数和奇数次方都映射到相同的表示向量。其次,r 的非整数值会产生复数向量。请注意,双极性向量是具有特定采样分布的复数向量的特例;我们将回到讨论不同分布如何影响 VFA 的属性。
4.2.2 具有循环卷积的 VFA
循环卷积是离散有限傅里叶变换 F 中使用的标准卷积操作,它可以用于从两个输入向量 x 和 y 生成一个向量:

对于傅里叶域中具有相位角

的任意相位向量。如果傅里叶空间中的相位向量是从平坦的相位分布(27)中采样的,傅里叶逆变换将产生复数值的向量分量,其中实部和虚部看起来像高斯随机变量分布。
然而,按照 Plate(1991)最初描述的,通过从高斯分布中独立地采样每个分量来产生基向量,并不是一个好策略,因为这些向量不太可能是完全酉性的。
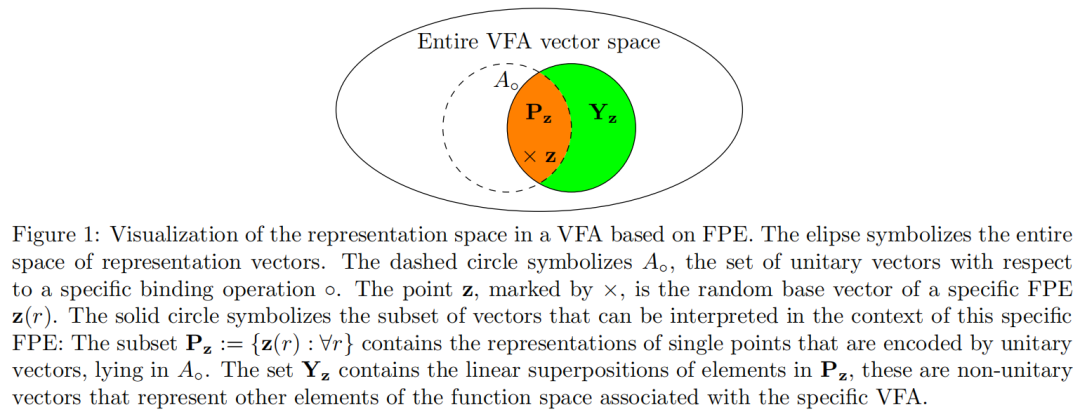
酉向量的一个显著子集是 one-hot 相位向量
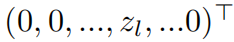
,它们是酉性的,因为它们的傅里叶变换是密集的相位向量:
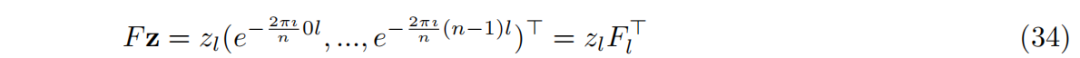
其中,
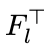
是离散傅里叶矩阵的第 l 列。因此,当傅里叶向量是离散傅里叶矩阵的列(具有恒定相位偏移)时,相应的基向量是单热的。此外,通常希望循环卷积中使用的基向量是纯实值的。这需要傅里叶域中采样的随机向量具有厄米对称性,即负频率的相量条目必须是相应正频率相量条目的共轭复数 (Komer et al., 2019)。
4.2.3 具有块局部循环卷积的 VFA
迄今为止描述的 VFA 的 FPE 基向量在具有哈达玛积绑定的模型中是完全稠密的相量,或在具有循环卷积绑定的模型中可以是最大稀疏的,即单热相量。可以在中间构建 VFA,其中 FPE 基相量向量具有期望的稀疏度级别 k < n。在这种结构中,基向量是稀疏块向量,具有 k 个大小相等的隔间,每个隔间是一个单热相量。以前,使用这种稀疏块向量的 VSA 被提出,使用所谓的块局部循环卷积 (LCC) 作为绑定操作 (Frady et al., 2021):


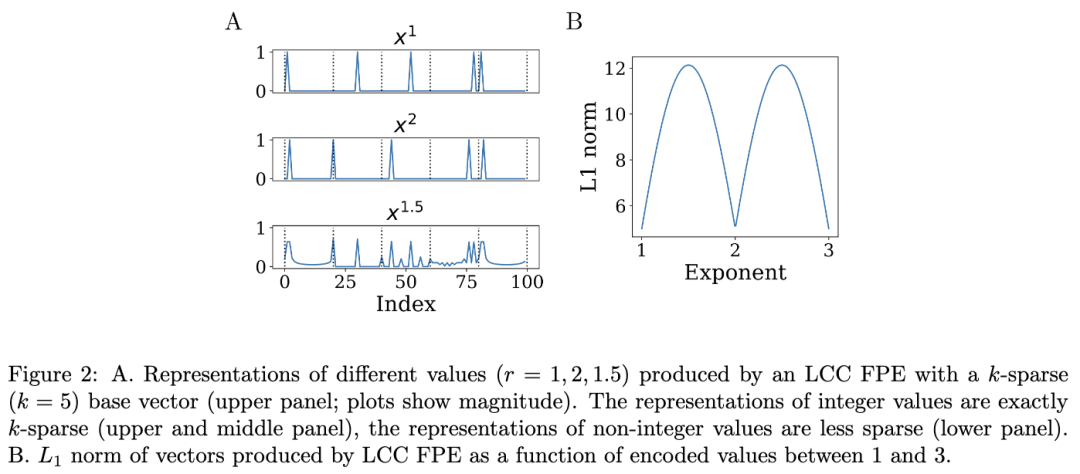
5 FPE的核
我们在第4节中看到,VSA和FPE的结合诱导了一个VFA。尽管这种模型之前已经被描述过,但它们在表示某些类别的函数和显式操作它们方面的能力并没有被充分利用。在本节中,我们分析了在这种VFA模型中可以实现的核属性。
5.1 具有均匀采样基向量的FPE具有通用核
形式上,FPE对于绑定操作的不同实现看起来非常不同。根据实现情况,它也需要不同的基向量。尽管如此,FPE具有一个通用的相似性核,如下定理所述。
定理2:假设有一个FPE,其基向量是均匀采样的,这是采样VSA向量的典型过程。对于Hadamard FPE,这意味着基向量的相位是从均匀相位分布中采样的,而对于CC FPE和LCC FPE,这意味着基向量在傅里叶域中对应于具有均匀相位分布样本的随机相位向量。然后FPE诱导了一个VFA,它是带限连续函数的RKHS,与绑定操作的底层实现无关。具体来说,FPE的核是sinc函数,它定义了带限连续函数的RKHS。
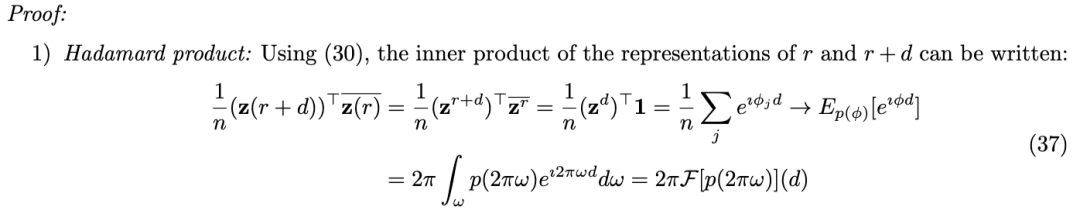



5.2 FPEs中塑造核 5.2.1 相位分布决定核形状

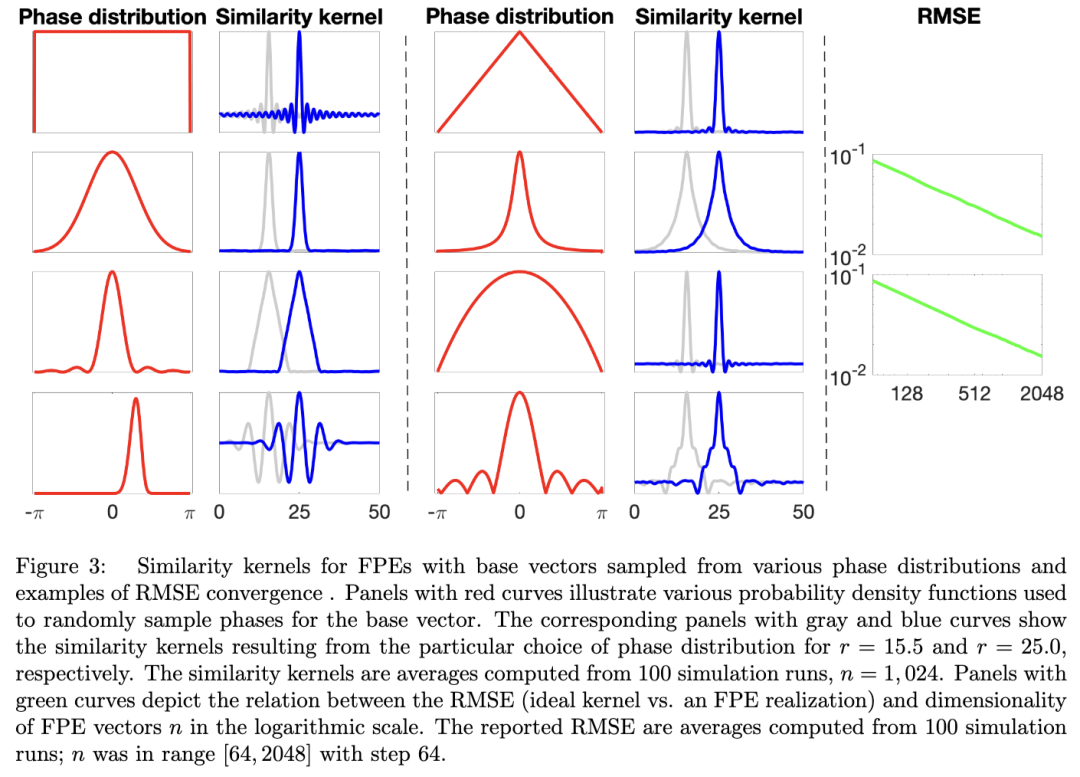
左上角面板描绘了具有均匀分布和 sinc 函数核的 FPE。其他面板显示,可以得到非常接近例如高斯(第二行左侧面板)、拉普拉斯(第二行右侧面板)或三角形(第三行左侧面板)核的相似性核。实际上,核的形状可以非常复杂,例如右下角面板中的核,其中相位的分布是使用截断的 sinc 函数绝对值定义的。此外,理想核与其 FPE 近似之间的 RMSE 随 n 指数衰减。
5.2.2 周期性核
根据 Bochner 定理,可以清楚地看出,周期性核将对应于离散傅里叶变换。通常,核的周期性由每个绑定操作的单位向量根的离散采样决定。在哈达玛绑定的情况下,周期性核是由基向量中的相量基向量产生的,其中每个分量是从离散化的相位分布中独立采样的。例如,周期性为 l 的核是由其各个相位均匀采样自 l 个相位值的基向量产生的,zi ∼ U{ei2πj/l, ∀j ∈ {1, ..., l}}。圆形流形上的数据可以通过相位值等于 1 的 l 次方根的基向量进行编码(参见图 4 示例)。通过在傅里叶域中采样离散相位,这些属性扩展到循环卷积绑定。当热相量元素也离散采样时,LCC 代码会产生循环。循环行为更复杂地取决于公共因数的乘积,具体取决于块大小和相位离散化。例如,如果块代码是纯二进制的(所有相位为 0),则循环周期将是块大小。
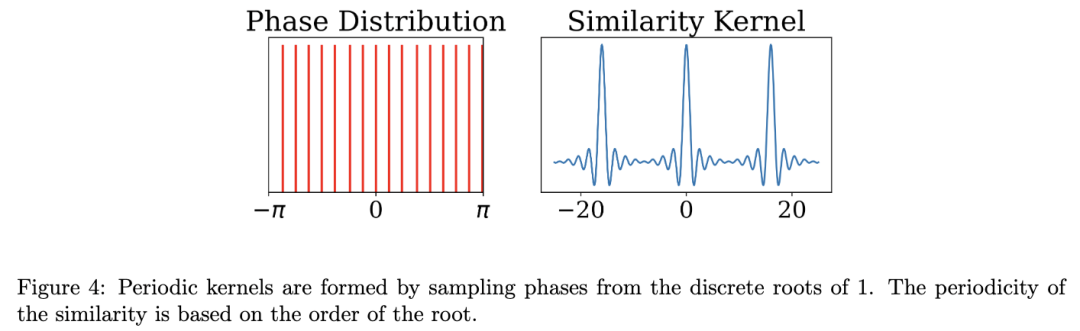
5.3 通过绑定形成的多维FPE
FPE可以扩展到编码多维数据空间:
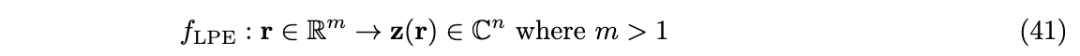
一种用于多维 FPE 的简单方法是将一维 FPE 进行笛卡尔组合,这一方法以前曾被提出(Weiss et al., 2016;Frady et al., 2018a)。笛卡尔结构涉及使用绑定操作对各个 FPE 进行正交化:
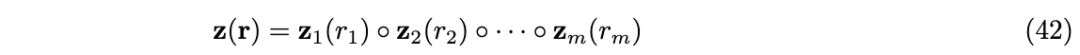

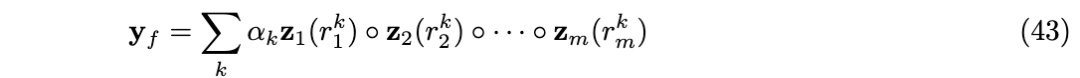
函数空间中的操作与一维VFA相同。
在大VSA维度的极限情况下,由多个具有sinc函数核的一维FPE形成的FPE的内积收敛于多维笛卡尔sinc函数:
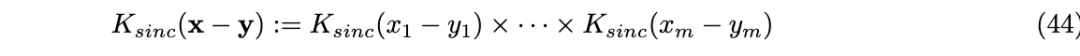
其二维傅里叶变换是一个方形。在图 5 中,通过绑定 (42) 组合的 FPE 与补充材料 A 中 Smolensky 张量积 (70) 组合的 FPE 进行了比较。由于哈达玛绑定可以被视为张量积的有损压缩 (Frady et al., 2021),因此哈达玛积方法收敛稍慢也就不足为奇了。然而,当在相同维度的表示上比较这些方法时,哈达玛积方法收敛得稍快一些(在 sinc 带宽内),见图 5D。请注意,对于有限的 VFA 维度,功率的最大偏差发生在 sinc 核的带宽内,因此高频失真和混叠效应相对较小。
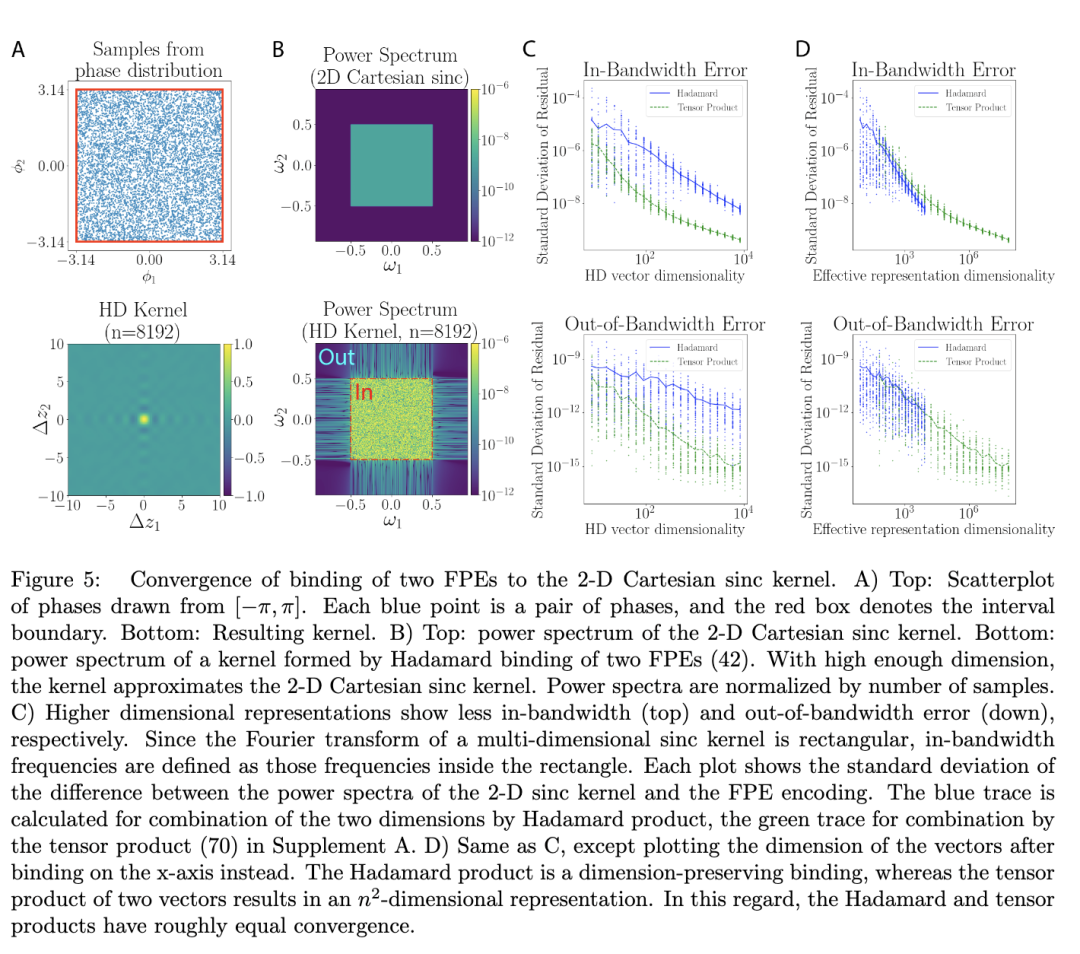
关于相对于哈达玛绑定的笛卡尔多维 FPE 的具体公式,见补充材料的第 A 节。
5.4 塑造多维FPE的核
多维核可以通过塑造构成它们的一维核来塑造,如第5.2节所述。进一步地,可以通过从联合相位分布中采样不同维度的FPE的基向量来产生非笛卡尔核,该联合相位分布不分解。
5.4.1 具有非笛卡尔结构的核
就像第5.2节中一维FPE的情况一样,Bochner定理可以用来塑造多维核。例如,可以产生具有非笛卡尔sinc核的FPE。Sinc核可以被概括为Brillouin区特征函数的傅里叶变换,在倒空间中是布拉维格子的一个原胞(Ye和Entezari,2011)。例如,六角形sinc核(见图6),可以从三个2-D笛卡尔sinc核组成:

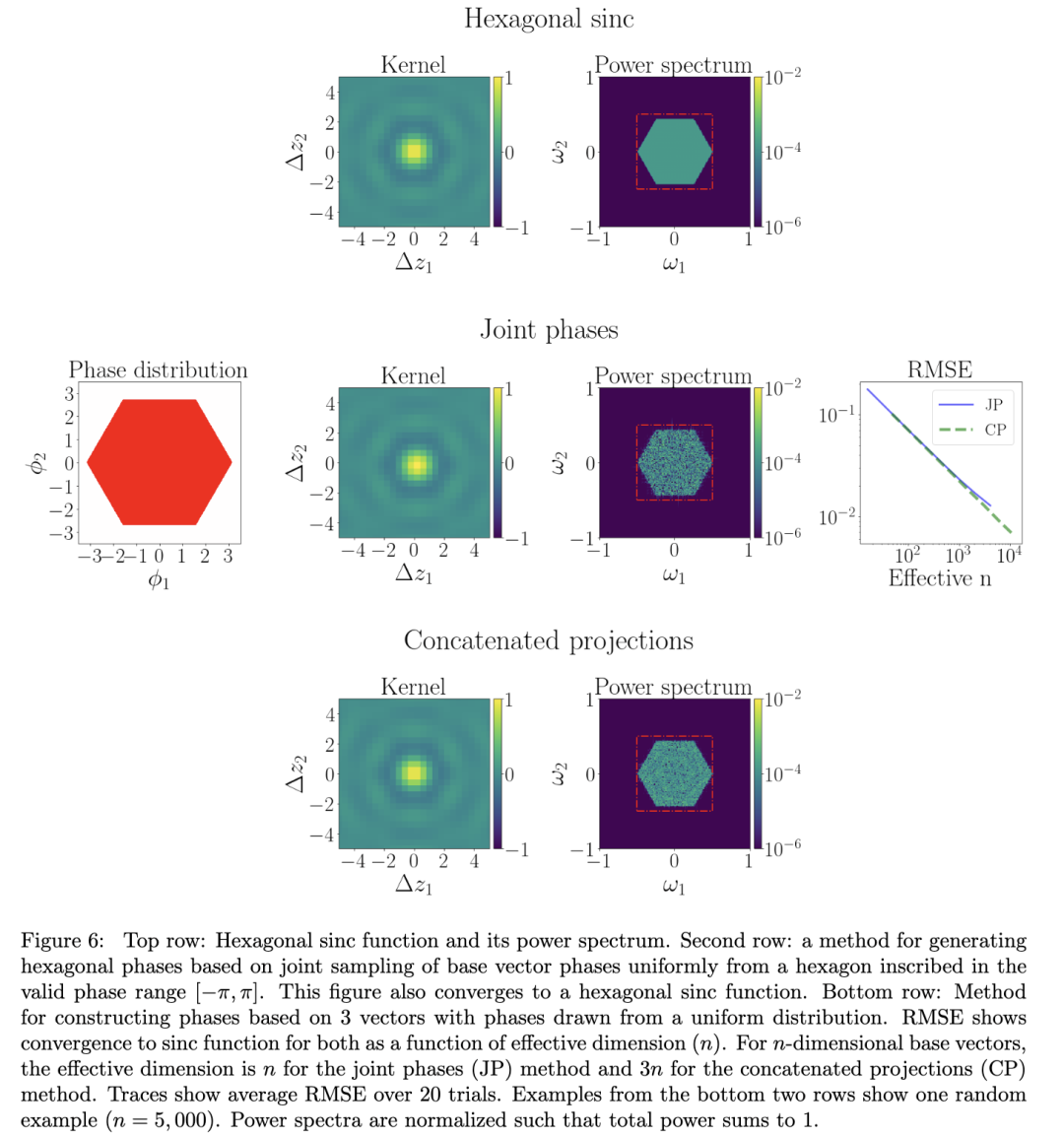
5.4.2 具有周期结构的非笛卡尔核
具有周期结构的核在工程和神经生物学导航系统中扮演着重要角色。
例如,在神经科学中,网格细胞是在海马体附近皮层记录中普遍观察到的现象(Hafting等人,2005),当动物探索环境时,这些神经元以规律的空间间隔发射,形成六角形晶格。在VFA中构建六角形晶格,可以利用晶体学的概念。晶体的分子可以通过布拉维格子来描述,由一组基向量乘以整数构建的理想网格。布拉维格子的傅里叶变换被称为倒格子,典型布拉维格子的倒格子是带限和离散的。因此,我们可以再次使用Bochner定理以及频率与相位的重新标记来构建具有理想网格细胞样模式的LPE。实际上,六角形晶格(图7,左上)只是二维布拉维格子的一种类型。通过选择沿其倒格子的相位,可以构建其他布拉维格子;示例见图7的前两行。
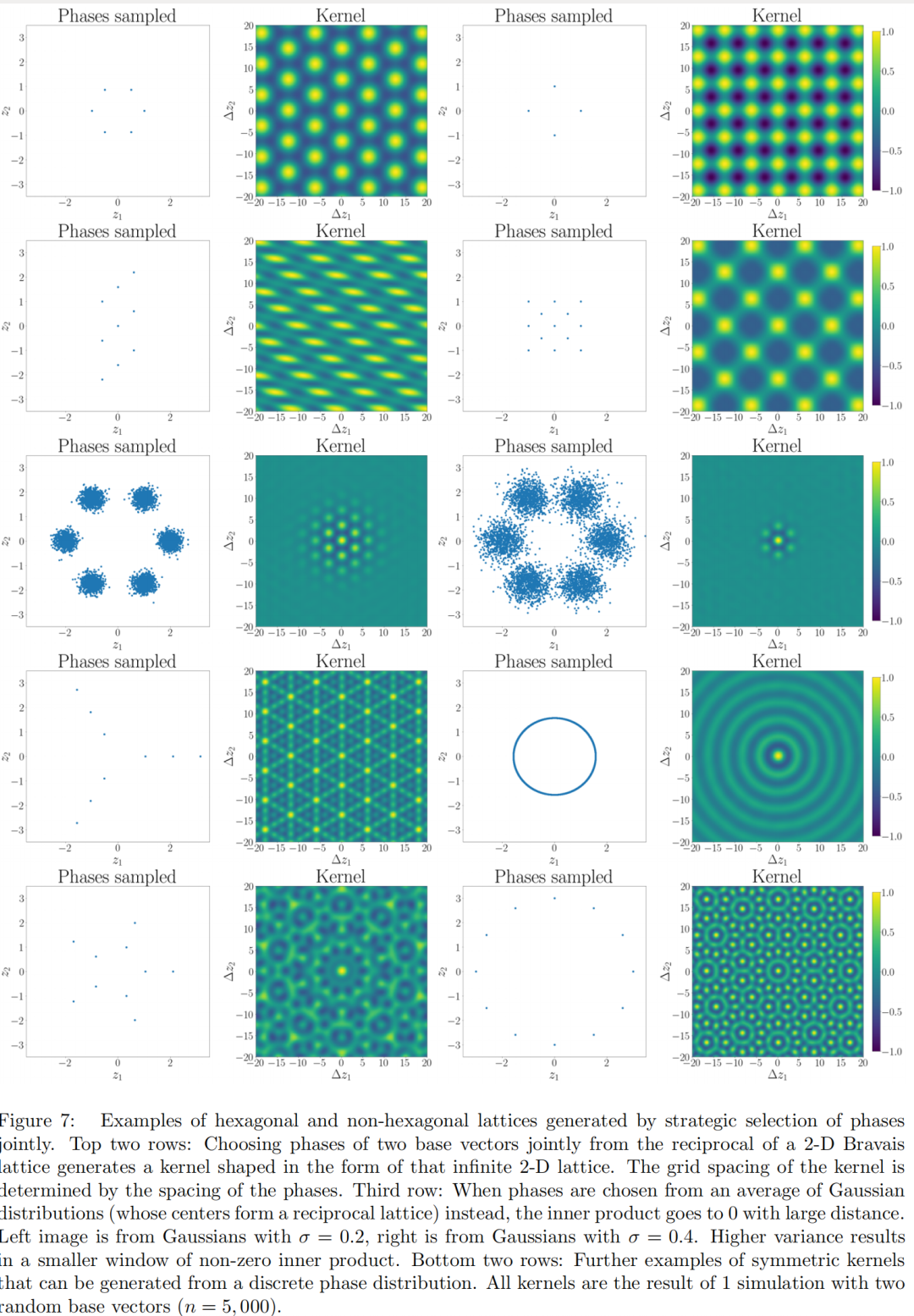
请注意,规则晶格只是离散带限函数的一个子集,图7的后两行展示了其他可能性。
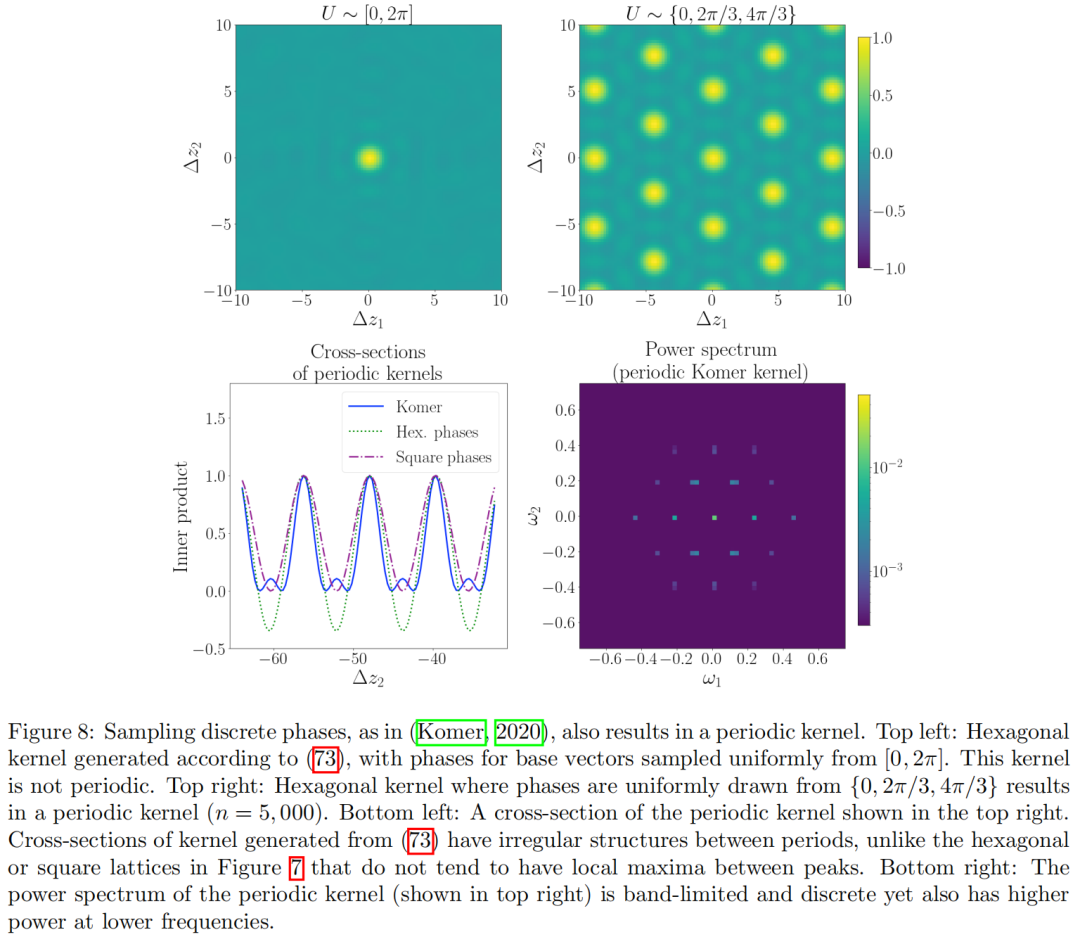
我们的方法与Komer (2020)提出的生成周期性核的方法相似,但并不完全相同。他们生成类似网格细胞核的方法是基于对基向量进行离散相位采样,这些基向量用在公式(72)中。这种方法的一个例子在图8中展示,由于其傅里叶变换也是带限和离散的,它的晶格看起来与我们在图7中展示的六角形晶格非常相似。然而,存在一些微妙的差异。例如,使用Komer (2020)的方法会在核的交叉截面的峰值之间产生局部最大值,而我们选择联合相位的方法则不会产生这些额外的局部最大值。
6 VFA中的检测、解码和去噪


VFA中的解码问题并不是一个新问题。在神经科学中,线吸引子网络被提出作为模型,用于说明神经回路如何解码、去噪和表示实数值输入。原则上,我们可以在VFA中使用线吸引子。这将需要一个电路,能够稳定并去噪给定基向量FPE的整个路径。然而,如何在线吸引子网络中存储特定FPE的路径尚不清楚。一个简单的解决方案可能是将路径细分得足够细致,并将得到的点存储在Hebbian联想记忆中。但这可能会失败,因为足够细致的路径细分可能会产生一组模式,这些模式太大,其成员之间的相关性太强,无法成功存储在Hebbian联想记忆电路中(Lewenstein和Tarkowski,1992)。
因此,这里我们提出了一个两步过程,用于包括粗匹配和精匹配步骤的检测和错误校正。对于粗匹配,我们在内容寻址存储器中存储路径上的锚点,见图9线上的点。形成路径的粗锚点,基向量以略小于2的间隔进行指数化,例如,
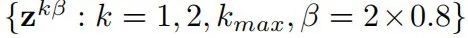
。
这种路径的离散化选择是为了使得路径上任何点的表示,其最近的锚点与其他锚点相比具有更高的内积。粗匹配步骤可以在相位联想记忆中完成,其中所有锚点都使用标准外积学习规则进行存储(Frady和Sommer,2019)。
一旦粗匹配步骤返回最近的锚点,第二个机制就精确地解码模拟值。这个机制涉及用于编码输入向量的FPE
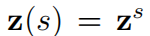
,以及一个电路,形成值s的表示和未知向量x之间的内积。
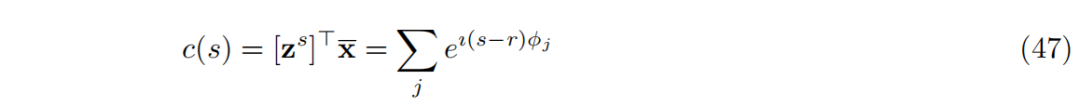

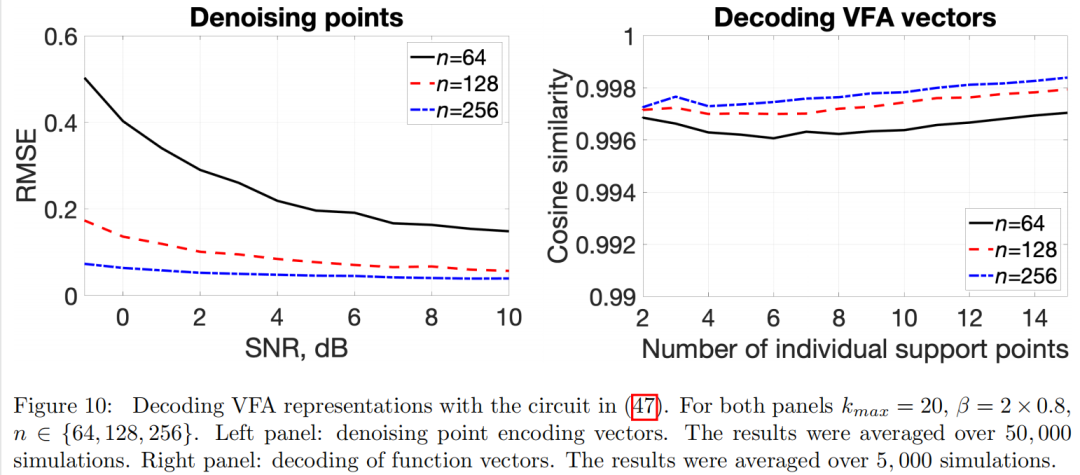

7 VFA应用示例到目前为止,我们已经展示了FPE在VFA中诱导了表示带限函数的向量。这里我们描述了这种类型的VFA在图像处理(第7.1节)、密度估计(第7.2.1节)和非线性回归(第7.2.2节)方面的具体应用。
7.1 图像数据处理
我们首先描述如何通过高维向量表示和操作图像数据,这是一个展示关键VFA属性的示例。本质上,我们将字母的简单图像视为图像域上的函数。为了简单起见,这个演示使用Hadamard VFA。图像平面中的位置通过二维FPE编码,基向量为x和y。为了避免平移时图像部分移出图像边界导致图像功率降低,我们希望函数空间具有环面结构,使图像边界无缝连接。为了实现这一点,我们通过选择如第5.4.2节中描述的离散相位分布中的基向量,来塑造一个周期性核。对于56x56像素大小的图像,x的相位从相位圆周上的56个离散点中选择,y也是如此。
字母图像是VFA函数空间中的一个元素,函数(11)的核展开中的每个项分别通过系数和支撑点编码像素的强度和位置,见图11的左图。多个字母可以通过添加各自的图像向量组合成场景(图11的中间图)。字母可以通过将每个图像向量与位置的分数幂编码绑定来放置在场景中。然后,可以通过第6节中描述的粗略搜索对场景向量进行解码:
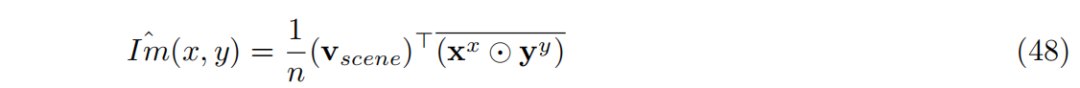
整个场景可以通过再次将场景向量与FPE平移向量绑定来移动。由于函数空间的环面结构,字母会在图像周围包裹。

7.2 VFA在非参数核方法中的模型 7.2.1 密度估计
VFA在密度估计中的应用可以借鉴早期在密度估计中使用sinc核的工作(Davis, 1975; Davis et al., 1977; Devroye, 1992; Glad et al., 2003; Agarwal et al., 2017)。
方法

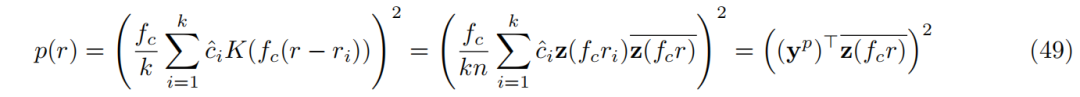
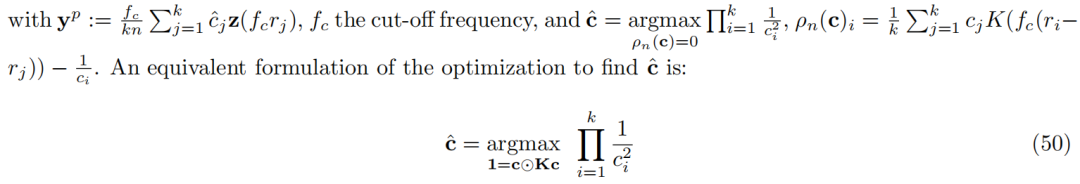
其中 1 是 k 维全一向量,K 是 k 个数据点的表示向量的文法矩阵。这个优化问题涉及到在 2^k 个局部最大值(每个象限一个)之间的穷尽搜索。为了避免这种昂贵的搜索,Agarwal 等人(2017)提出了三种近似解决方案算法。在下面的实验中,我们使用了 BLMLTrivial 算法。如果 p(x) 确实是带限的并且严格为正,则这个算法会渐近地收敛到真正的 BLML 估计器。
实证评估
我们使用 Agarwal 等人(2017)的一个替代概率密度函数(pdf)的例子:


图12展示了随着向量维度增加,VFA估计质量的提高。
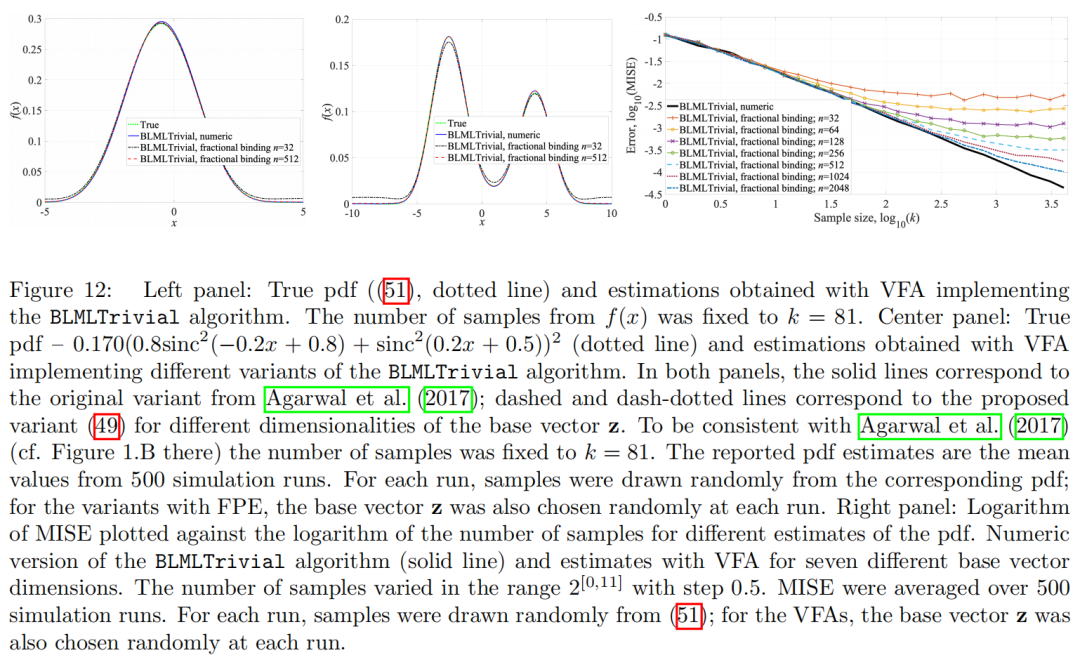
虽然向量维度 n = 32 能够对整体曲线形状提供合理的估计,但会高估尾部,对于向量维度 n = 512,即使在尾部,估计值也接近真实情况。
因此,VFA的维度影响估计质量。这一观察结果使得进行了下一个实验,在该实验中,样本数量 k 和维度 n 被共同变化。
注意,在图12的右图中,BLMLTrivial算法的数值实现的MISE(粗实线)随着样本数量的增加而稳定下降。这种下降反映了随着数据限制逐渐解除,精度的提高。VFA模型的MISE曲线跟随这条曲线,但在某个点上偏离实线并趋于平稳。在实践中,这具有以下后果。
在无限数据的情况下,即对于大量的样本,VFA模型的精度随着其维度的增加而稳步提高。这种随维度提高的精度在经典VSAs中也已被观察到,并被称为“维度的恩赐”(Gorban和Tyukin,2018)。
在数据有限的情况下,即对于少量的固定观测点,情况就大不相同了。在这种情况下,具有足够大的固定维度的VFA已经达到了数值变体的相同性能。在这一点之后增加维度不会进一步提高性能。因此,在数据有限的情况下,可以将VFA的维度限制在某个固定值,而不会损害性能。
7.2.2 非线性回归
为了演示使用VFA的非参数非线性回归,我们可以借鉴一些关于使用sinc核进行回归的先前文献(Bissantz和Holzmann,2007;Exterkate,2011;Bousselmi等人,2020)。


实证评估
为了展示基于FPE的非参数非线性回归方法及其数值对应方法,我们使用了与Bousselmi等人(2020)中相同的合成数据(参见其中的例子1):
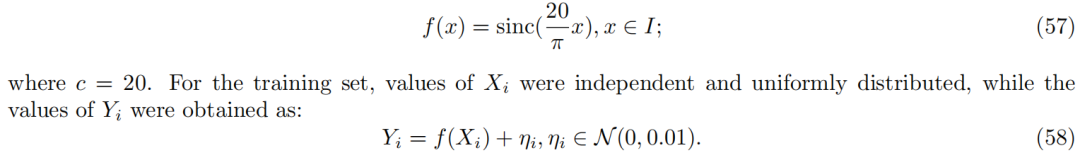
遵循Bousselmi等人(2020)的设置,经验投影方法的c值设定为20,而对于Tikhonov正则化方法,参数为:c = 30,λ = 0.01。
这个实验展示了两种正则化方法的VFA实现都能够对目标函数(图13的左图)提供合理的估计。与经验投影VFA相比,Tikhonov VFA实现了更低的均方根误差(RMSE)。然而,这种改进是以增加计算成本为代价的,因为Tikhonov VFA需要解决(55)。
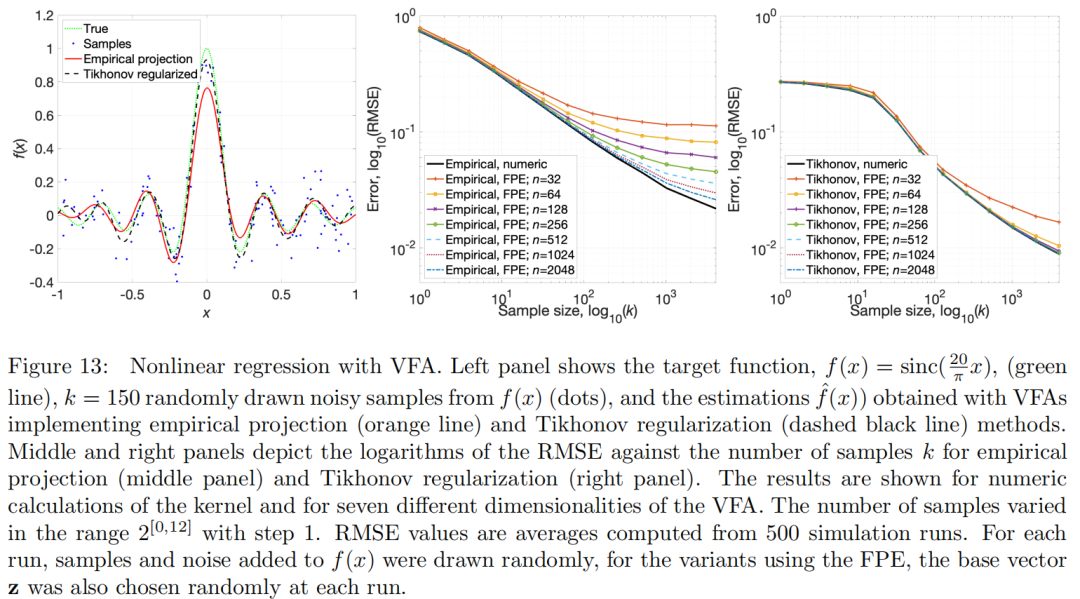
关于性能随可用数据点数量和VFA维度的扩展,我们观察到了与密度估计相似的趋势。误差随着k和n的增加而减少,对于固定的k,存在一个最小的维度可以达到最佳性能。有趣的是,对于最佳性能所需的VFA大小,Tikhonov VFA明显小于经验投影VFA。
8.4 相关著作
虽然我们相信我们是第一个正式定义VFA模型并描述它们表示和操作函数的能力的人,但是还有相关的前期工作。
8.4.1分数功率编码Fractional Power Encoding (FPE)在VSA的早期应用
早期将VSA和FPE合并的提议已经指出了许多有趣的应用。例如,Plate (1992)提出了基于循环卷积绑定的分数幂向量,作为在递归神经网络中表示离散序列的机制。推广分数功率向量,在VSA中提出了基于圆卷积的FPE,用于表示2-D空间中的连续轨迹(Plate (1994a)中的5.6节)。在以下应用的背景下,VSA和循环卷积FPE4的组合在许多最近的论文中被重新讨论:
•对二维图像的推理:Weiss等人(2016年)使用这种模型来整体表示二维图像,从而提供了查询图像的可能性,即回答关系查询,如“哪个数字在2的下面和1的左边?”在包含MNIST数字数组的图像中。Frady等人(2018年b)也描述了类似的图像推理模型;陆等(2019)。我们在该应用领域中的示例演示了如何调整VFA的核形状以最佳地适应该应用,即,形成用于提供环形边界条件的周期核,参见第7.1节。
•在二维环境中导航:Weiss等人(2016)展示了FPE在解决导航问题中的应用,Komer和Eliasmith (2020)进一步阐述了这一应用。
•神经形态计算模型:有一些在神经形态计算中使用这种模型的初步尝试。在Frady等人(2018a)的研究中,Hadamard FPE被用于海马体模型,该模型将脉冲神经网络中的计算和基于节律的时序模式联系起来,而Dumont和Eliasmith (2020)提出了一种通过脉冲神经元的速率实现FPE向量的方法。
动态系统的预测:Voelker等人(2021年)建议使用该模型来模拟和预测动态系统的行为。
4在Komer等人(2019)中,结合这些元素的模型被称为“空间语义指针”,扩展了同一研究小组将VSA表示称为“语义指针”的惯例(Blouw等人,2016)。