
摘要
本文提出了一个表示高保真点云传感器观测的框架,用于实现高效的通信和存储。该方法利用稀疏高斯过程将点云进行压缩编码。我们的方法只使用一个模型(一个2D稀疏高斯过程)来表示自由空间和被占据空间,而不是现有的双模型框架(两个3D高斯混合模型)。我们通过提出一种基于方差的采样技术来实现这一点,它可以有效地区分自由空间和被占据空间。这种新的表示方式需要更少的内存占用,并且可以通过有限带宽的通信通道进行传输。该框架在仿真中被广泛应用,并被一个配有3D激光雷达的真实移动机器人进行了验证。与发送原始点云相比,我们的方法使通信速率降低了70~100倍。
一、简介
随着激光雷达技术的快速发展,我们现在可以建立具有非常高分辨率的地图。例如,只有一个16通道的3D激光雷达的每一次全扫描可以给我们代表周围障碍物的57600点,然而,使用高分辨率激光雷达的一个代价是绘制环境地图时的计算、存储和通信成本。虽然人们可以通过使用高性能的计算机系统来升级计算和存储,但由于可用的通信带宽较低,通信通常会成为一个瓶颈。在实践中,低带宽通信被认为是许多机器人应用的主要挑战,如水下和地下环境(洞穴、隧道、矿山等)的占用测绘,在通信基础设施退化的灾难场景中的搜索和救援任务,以及行星探索任务。低带宽可以阻止机器人实时共享其传感器观测结果,如果机器人需要跟踪或与外部控制或监督平台交互,则会显著降低系统的响应能力。这项工作解决了通过有限带宽的通信信道共享高保真的三维点云问题。

图1:系统概述
我们所考虑的系统由一个配备了激光雷达和通信设备的机器人组成,并部署在一个低带宽的环境中。它获得的观测结果是建立环境占用图的基础,见图1。我们的方法利用变分稀硫高斯过程作为一个生成模型,以一个紧凑的形式表示点云。这种轻量级表示通过低带宽通信传输到原始点云重建的基地。大量的评估显示,我们的方法减少了70~100倍的内存以及传输点云数据所需的通信速率。
二、背景
GP 是非参数模型,由均值函数 m ( x )和协方差函数(核函数) k ( x , x ′)表示,其中 x 为 GP 输入[27]:
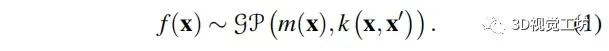
考虑一个数据集

,有 N 个实训输入 x 和它们对应的标量输出(观察值)y。在使用数据集 D 代表 GP 后,任何新的查询

的输出
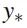
都可以使用 GP 预测来估计:


和
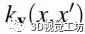
是后验均值和协方差函数[2]。GP 预测方程依赖于超参数

的值,其中

是核参数,
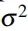
是噪声方差。
一个完整 GP 的计算复杂度为

。为了降低计算复杂度,文献中提出了不同的近似方法,只考虑 M 个输入点来表示整个训练数据[27]。这些输入点被称为诱导点

及其对应的底层值函数 f(x)称为诱导变量

。将整个数据集替换为 m 诱导输入会导致 SGP 的计算复杂度为

。图西人[2]提出了一个变分学习框架联合估计核超参数和归纳点。图西人的框架通过变分后验分布

近似于GP

的真实后验。

其中

为自由变分高斯分布。用
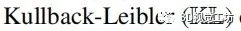
散度来描述近似后验与真实后验之间的差异。最小化近似值和真实后验

相当于最大化真实对数编辑似然的变分下界:
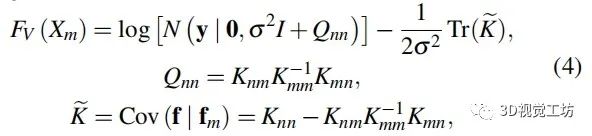
其中

是变分目标函数,

是正则化迹项,Knn 是原始的 n×n 协方差矩阵,Kmm是诱导输入上的 m × m 协方差矩阵,Knm是训练点和诱导点之间的 n×m交叉协方差矩阵,
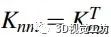
。关于 VSGP 的更多细节可以在图西人的作品中找到。
三、方法
该方法利用 VSGP 作为生成模型来编码3D点云。在不同的 GP 近似方法中选择 VSGP 的原因如下:
1)变分逼近区分了诱导点 M (作为变分参数)和核超参数

2)变分目标函数(Eq.④)中的正则化项

对超参数进行正则化避免数据过拟合。
3)变分逼近提供一种从原始数据中选择诱导输入

的离散优化方案。
4)VSGP 作为占用面生成模型
我们将测距传感器(例如激光雷达)观察到的占用点投影到传感器原点周围具有预定义半径

的圆形表面上。有关诱导点选择的更多信息,请参阅[2] 这个曲面称为占用曲面,见图3。在我们的方法中,传感器观测定义在球坐标系中,中任何观测点都由元组
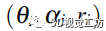
描述,元组分别表示方位角、仰角和半径值。同样,任何点云数据都可以使用以下公式从笛卡尔坐标
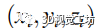
转换为球坐标
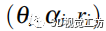
,用公式:


所有位于圆形占用曲面外(半径

)或曲面上(半径
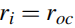
)的观测点均被忽略,视为自由空间。其余位于圆形曲面内部(半径

)的点被投影在占用曲面上,称为被占用点。因此,占用面半径作为传感器的最大范围。表面上的每个占用点由两个属性:方位角和仰角

,并分配了一个占用值

,它是关于点半径的函数。占用面上各点的占用概率
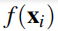
由 VSGP 建模:

考虑到噪声测量,我们在占用函数
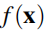
中添加白噪声,因此观察到的占用被描述为

,其中服从高斯分布

。占用率曲面的最终模型是一个二维 VSGP ,其中输入是方位角和仰角,

,相应的输出是预期占用率。
B.基于方差的抽样
重构过程通过一个与定位子侧的 VSGP 配置相同核( RQ )和似然(高斯)的 GP 完成。基础 GP 接受在诱导点上训练。计算复杂度为

,其中 M 为诱导点的个数,故称其为稀疏 GP ( SGP ),将重建的占用曲面称为 SGP 占用曲面。生成一个由激光雷达在方位角和仰角轴上具有相同分辨率的查询点组成的网格
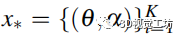
,从 SGP 占用面重建原始点云——我们将重建的点云称为 SGP 点云。如果由于任何原因需要对点云进行上采样,则可以使用具有更高分辨率的查询网格进行重建过程。利用 SGP 占用曲面预测每个点的占用率

的查询网格。将占用率转换回球半径
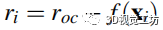
,还原每个点的三维球坐标。
与其他建模技术相比, GP 及其变体的一个优势是与任何查询点的预测值相关的不确定性(方差)。考虑到侦察方占用面的 VSGP 模型,与占用点相关的方差相比,与空闲点相关的方差较低。从原始占位点中选取诱导点集合,可以保持基底侧重建 SGP 占位曲面的占位部分的低方差值。因此,使用重建 SGP 占用曲面上任意点的方差值

进行预测。事实上,与占用面相关的方差在不同的观测中是不同的,它受到观测(占用)点的数量及其在占用面上分布的影响。因此,我们选择方差阈值

作为变量,它随着方差在占用面被占用部分和空闲部分上的分布而变化。

定义为曲面上方差均值和标准差

的线性组合,即

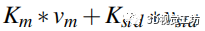
,其中
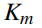
、

为常数。首先设置

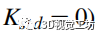
,对这两个常数进行调优,然后逐渐增大

,减小
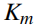
,直到得到重建 SGP 点云精度最高的数值(考虑固定数量的诱导点)。
四、实验结果
我们根据在侦察机和基地之间传输传感器观测数据所需的内存减少和通信速率来评估我们方法的性能。VSGP 表示仅需要 1514 个浮点 (FP) 来表示整个点云(每个诱导点 (3x500) 3 FP + 机器人姿势 6 FP + 超参数 6 FP)。该值小于 GMM 方法所需的内存,后者需要 ∼ 2000 FP(每个组件 (10x200) 10 FP 分布为 6 FP 协方差 + 3 FP 均值 + 1 FP 权重)。
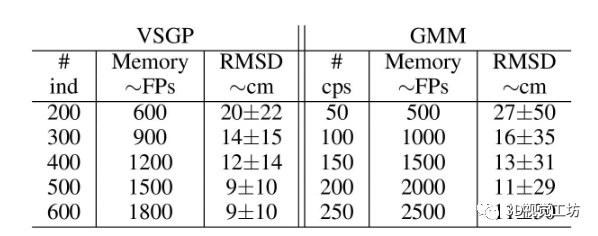

图 d 表明,对于一对匹配的 GMM 和 VSGP,GMM 的采样时间比配对的 VSGP 少。然而,VSGP 的点云重建过程比 GMM 方法更方便,因为 VSGP 和 GMM 采样之间的根本区别在于:当我们从 GMM 采样时,我们得到一个具有随机值 θ的样本(来自分布)(θs, rs),因此我们无法控制样本在占用表面上的位置 (θs ,αs)。相反,对于 VSGP 方法,我们预测由(θs ,αs) 定义的占用表面上某个点的半径值 rs。因此,我们可以控制占用表面上的点位置。在使用 scout-base 方案构建隧道环境的 3D octomap 时,发送原始点云、GMM 编码数据和 VSGP 编码数据的平均通信速率分别为 1750 KB/S、25.8 KB/S 和 18.2 KB/S分别见图 6d。通过网络发送的累积数据从发送原始点云的 840 MB 减少到 GMM 的 12.4 MB 和 VSGP 的 8.7 MB。
总结
文我们介绍了使用 VSGP 的 3D 点云的轻量级表示。这种表示允许通过有限带宽的通道有效地存储和传输高保真观测值。基于模拟和硬件实验的结果,我们的方法使传感器观察的尺寸表示缩小了大约 70-100 倍。这种紧凑的表示可以促进许多受通信带宽限制的机器人应用,例如地下和水下探索、搜索和救援任务以及行星探索。此外,我们的方法在多机器人协作的环境中也很有用,在这种情况下,许多机器人需要通过低带宽通道共享大量信息(3D 点云)。