问题描述:
对于任意方阵,其行列式(determinant)为一个标量,可以看作线性变换对体积的影响或扩大率,行列式的正负号对应图形的镜像翻转。2阶方阵的行列式表示每列向量围成的平行四边形的面积,3阶方阵的行列式表示每列向量围成的平行六面积的体积。在多重积分的换元法中,行列式起到了关键作用。在研究概率密度函数根据随机变量的变化而产生的变化时,也要依靠行列式进行计算,例如空间的延申会导致密度的下降。另外,行列式还可以用来检测是否产生了退化,表示压缩扁平化(把多个点映射到同一个点)的矩阵的行列式为0,行列式为0的矩阵表示的必然是压缩扁平化,这样的矩阵肯定不存在逆矩阵。

把矩阵的某一行(或列)乘以一个标量然后加到另一行(或列)上,矩阵的行列式不变,交换任意两行(或列)后行列式的值变为相反数。上三角矩阵和下三角矩阵的行列式等于对角线元素的乘积,可以使用高斯消元法把任意矩阵转换成上三角矩阵然后计算行列式。
一种计算矩阵行列式的方法为,

参考代码:

运行结果:

在上面的程序中,使用标准库itertools中的函数permutations()生成全排列。如果想自己实现全排列算法(一般不建议这样做),可以参考下面的代码。

运行结果:




参考代码:
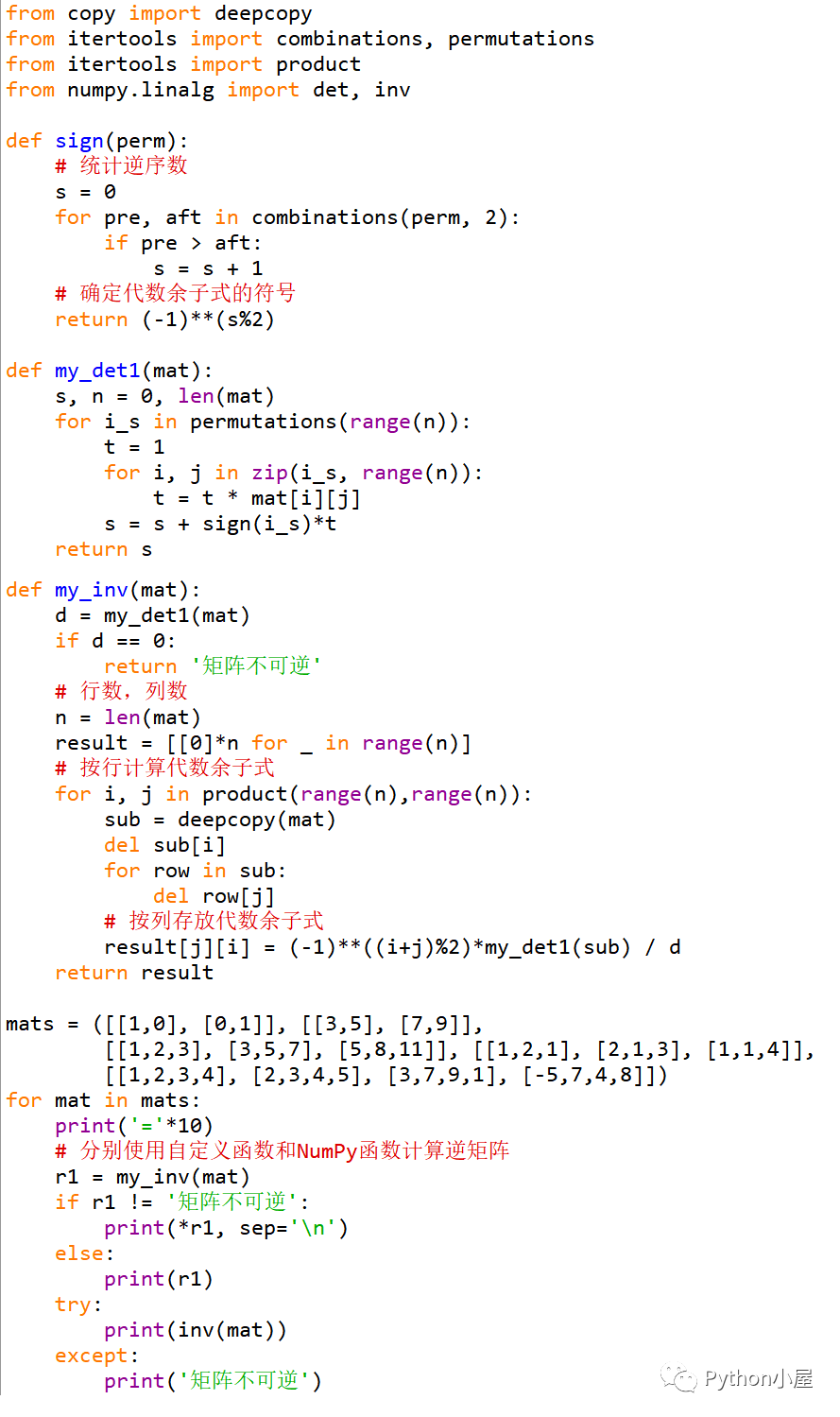
运行结果:
