
本文介绍来自北京航空航天大学彭浩老师团队发表在Artificial Intelligence Journal(AIJ) 2024上的一篇文章“Incremental Measurement of Structural Entropy for Dynamic Graphs”。为了解决目前的方法不支持动态编码树更新和增量结构熵计算的问题,作者提出一种新的增量度量框架 - Incre-2dSE,它可以动态调整群落划分,支持更新的二维结构熵的实时测量。作者在人工和现实世界的数据集上进行了广泛的实验,实验结果证明,该增量算法有效地捕捉了社区的动态演变,减少了时间消耗,并提供了良好的可解释性。 论文名称:Incremental Measurement of Structural Entropy for Dynamic Graphs 论文链接:https://doi.org/10.48550/arXiv.2207.12653 代码链接:https://github.com/SELGroup/IncreSE
1. 引言
近年来,有学者提出一种基于编码树的图结构信息度量,即结构熵,用于发现图中嵌入的自然层次结构。结构熵在生物数据挖掘、信息安全、图神经网络等领域得到了广泛的应用。
在动态场景中,一个图在时间序列中从初始状态演变为许多更新的图。为了有效地度量不断变化的群落划分的质量,我们需要在任何给定时间增量地计算更新的结构熵。不幸的是,由于两个挑战,目前的结构熵方法不支持有效的增量计算。
挑战 1:为每个更新的图重建编码树将导致大量的时间消耗
为了解决这个问题,作者提出了两种二维编码树的动态调整策略,即朴素调整策略和节点移位调整策略。前者保持原有的社区划分,支持理论结构熵分析;后者基于结构熵最小化原则,通过在社区之间移动节点,动态调整社区划分。
挑战 2:传统定义的结构熵计算具有较高的时间复杂度
为了解决这个问题,作者设计了一个增量框架,即 Incre-2dSE,用于有效地测量更新的二维结构熵。具体而言,Incre-2dSE首先利用两种动态调整策略生成调整量,即重要统计量从原始图到更新图的变化,然后利用调整量通过新设计的增量公式计算更新后的结构熵。此外,作者还将增量方法推广到无向加权图,并对有向加权图的一维结构熵的计算进行了详细的讨论。
2. 方法
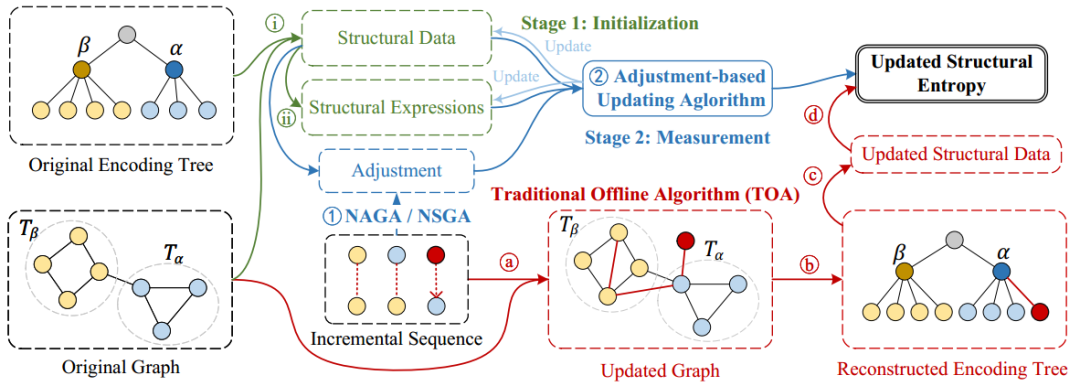
图 1 Incre-2dSE框架图。
2.1 二维编码树的动态调整策略
2.1.1朴素调整策略
朴素调整策略包括两部分:边缘策略和节点策略。边缘策略规定增量边不会改变编码树的结构;节点策略规定,当一个新节点 与已有节点 连接时,且 对应二维编码树中的叶节点 ,即 时,将设置一个标签为 的新叶节点 作为 父节点的直接后继节点,而不是另一个1高度的节点。我们可以从群体的角度来描述编码树的修改。具体来说,增量边不改变现有节点的社区,而新节点被分配到其邻居的社区,而不是另一个任意社区。显然,给定大小为 的增量序列,我们可以在时间复杂度为 的情况下得到更新后的编码树,即更新后的群落划分。
在这一部分中,作者引入了全局不变量和局部差分两个量,通过朴素平差策略实现了更新结构熵的逼近和快速增量计算。对图 施加大小为 的增量序列 ,采用朴素调整策略得到新的图 及其对应的二维编码树 ,更新后的二维结构熵可表示为:
然而,增量大小 会影响上式中求和方程中的所有项。因此,更新和计算过程的成本至少为 ,当图变得非常大时,这个成本是巨大的。一种直观的尝试是在更新的结构熵和原始的结构熵之间做出区别,试图在 中计算增量熵。然而,由于在上式的所有项中 都变为 ,因此很难从差分方程中推导出简洁的 公式。为了解决这个问题,作者在这里引入了全局不变量和局部差分。作者将全局不变量定义为近似更新的结构熵,局部差分定义为更新后的结构熵与全局不变量之差,也可视为近似误差。总的来说,通过计算和求和全局不变量和局部差分,可以在 内计算出更新后的二维结构熵。
2.1.2节点移位调整策略
虽然朴素调整策略可以快速获得更新后的二维编码树及其相应的结构熵,但我们仍然需要一种更有效的策略来获得较低结构熵的更好的群落划分。因此,作者提出了另一种新的动态调整策略,即节点移位,通过迭代地将节点移动到其最优偏好社区。与单纯调整策略不同,边缘变化可以改变现有节点的群落,使结构熵最小化。此外,该策略支持同时增加多个边和删除现有边。因此,节点移位调整策略完全克服了朴素调整策略的局限性。
首先将最优偏好社区(OPC)定义为目标节点的最佳社区,即如果目标节点进入其OPC,则总体二维结构熵与OPC以外的其他社区相比必须最低。则节点移位调整策略可描述为:(1)设涉及节点为增量序列中出现的所有节点;(2)对于每个涉及的节点,将其移动到其OPC;(3)将涉及的节点更新为与移位节点连接但在不同社区的所有节点,然后重复步骤(2)。
2.2 Incre-2dSE:增量测量框架
图1展示了增量测量框架(包括初始化和测量两个阶段)和传统离线算法(TOA)。Incre-2dSE的目的是在给定原始图、原始编码树和增量序列的情况下,在动态调整社区划分的同时,有效地度量更新后的二维结构熵。
2.2.1 阶段1:初始化
给定图 为稀疏矩阵,其二维编码树由如下字典表示:{社区ID 1:节点列表1,社区ID 2:节点列表2,…}时,可以很容易地获取并保存结构数据,其时间复杂度为 。然后使用保存在 中的结构数据计算结构表达式。总的来说,初始化阶段需要总时间复杂度为 。
2.2.2 阶段2:测量
在这个阶段,我们首先需要生成从 到 的调整。通过提出的两种动态调整策略,作者提供了两种算法来生成调整量,即朴素调整量生成算法(NAGA)和节点移位调整量生成算法(NSGA)(图1中的①)。两种算法的输入都是原始图的结构数据和一个增量序列,输出是一个调整。NAGA的时间复杂度为 ,因为它需要在增量序列中遍历 条边,而每条边只需要花费 。在NSGA中,我们首先需要 来初始化调整。其次,在节点移动部分,我们需要确定所有涉及节点的OPC,这需要花费 。此步骤重复 次,时间开销为 ,其中 表示第 次迭代中涉及的节点数。由于大多数情况下 和 ,所以NSGA的总时间复杂度为 。
得到调整值后,可以增量计算更新后的二维结构熵:
为了实现上述增量计算过程,作者还提供了基于调整的增量更新算法(AIUA)(图1中的②)。给定输入,即原始图的结构数据和结构表达式以及更新后的图的调整,我们可以增量计算更新后的二维结构熵,并在新的调整到来时有效地更新结构数据和结构表达式,为下一个AIUA过程做好准备。更新结构数据的时间复杂度为 。更新结构表达式的时间复杂度为 。计算更新后的二维结构熵的时间复杂度为 。综上,AIUA的总时间复杂度为 。
2.3 基线:传统的离线算法(TOA)
传统的离线算法(TOA)对每一个更新的图重构编码树,并通过定义计算更新后的二维结构熵。TOA由以下四个步骤组成。首先,将原始图与增量序列结合生成更新后的图(图1中的a)。其次,使用几种不同的静态社团检测算法,如Infomap、Louvain、Leiden,将图节点集划分为社团,构建二维编码树(图1中的b)。第三,对更新后的图的节点级、社团级、图级结构数据进行计数并保存(图1中的c)。更新后的结构熵通过式1计算(图1中的d)。TOA的总时间成本为 加上所选社团检测算法的成本。
作者给出了传统离线算法的伪代码,如下图所示:

图 2 传统离线算法的伪代码。
2.4 复杂图的扩展
作者在文章中讨论了将此方法扩展到无向加权图或有向图的可行性。首先,作者论证了无向加权图的方法可以由无向无权图的方法自然推广。其次,分析了有向图结构熵增量计算范式与无向图结构熵增量计算范式的根本区别,提出了有向加权图一维结构熵增量计算的新方法。
无向加权图:无向加权图结构熵的增量测量方法可以直观、方便地从之前提出的无向无权图结构熵增量测量方法中扩展出来。作者首先介绍了无向加权图的二维结构熵的定义。在此基础上,更新了结构熵调整的定义,提出了新情况下结构熵计算的增量公式。
有向图:由于有向图的结构熵测量与无向图的结构熵测量有本质的不同,本文提出的主要方法难以转移到有向图场景中。关键的区别在于有向图需要转换成一个转移矩阵,而平稳分布需要计算。由于二维结构熵的增量计算非常复杂,在这一部分中,作者简要地提出了一种测量有向权图一维结构熵的增量方案。具体来说,首先定义了有向加权图及其非负矩阵表示。然后,引入了有向加权图的结构熵公式。最后,回顾了有向加权图一维结构熵精确或近似计算的传统方法,即特征向量计算和全局聚合,并提出了一种增量迭代逼近算法,即局部传播算法,如图3所示。
在全局聚合中,每次迭代都需要遍历所有的节点和边,这导致了很高的计算冗余。在这一部分中,作者提出了一种快速逼近更新后的一维结构熵的新方法,即局部传播。顾名思义,其关键思想是在下式(3)中使用仅涉及改变的局部节点的信息传播方案,进一步降低聚合过程的冗余度。
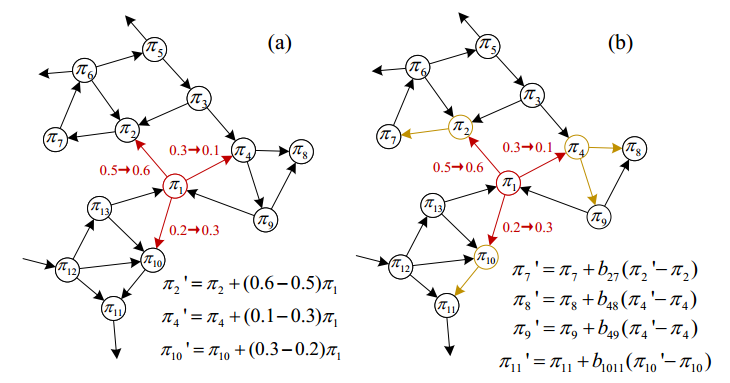
图 3 局部传播算法的示意图。
3 实验与评估
作者基于动态图形实时监控和社区优化的应用进行了广泛的实验。
3.1 数据集介绍
人工数据集:首先,作者利用“Networkx”(一个Python库)中的随机分区图(random)、高斯随机分区图(gaussian)和随机块模型(SBM)方法生成动态图的3种不同初始状态。之后,通过Hawkes Process对每个初始状态生成增量序列和更新图。霍克斯过程通过假设历史事件可以影响当前事件的发生,对离散序列事件进行建模。
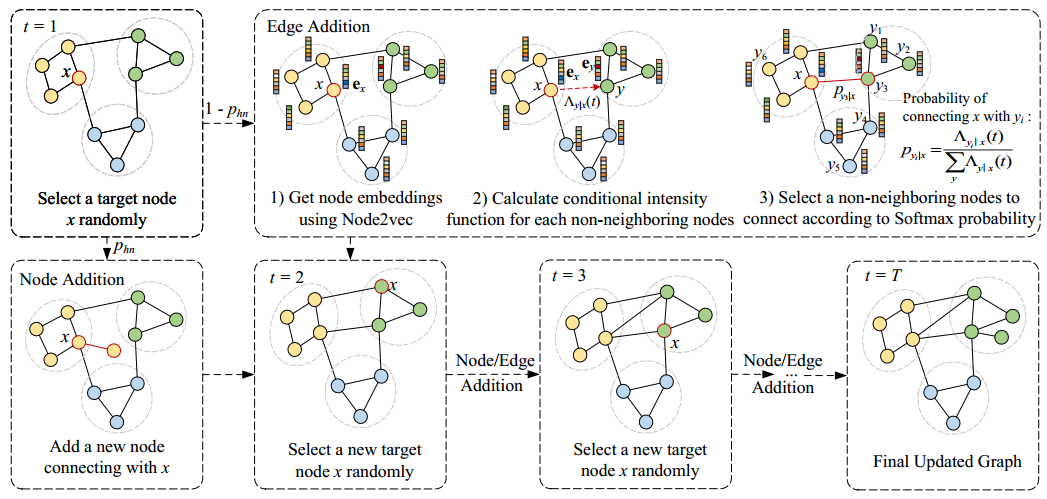
图 4 人工Hawkes数据集生成过程。
真实数据集:对于现实世界的数据集,作者选择了Cit-HepPh、DBLP和Facebook进行实验。对于每个数据集,作者截取了21个连续的快照(一个初始状态和20个更新的图)。由于结构熵仅在连通图上定义,因此只保留每个快照的最大连通分量。总的来说,图5简要显示了人工数据集和真实数据集的统计数据。
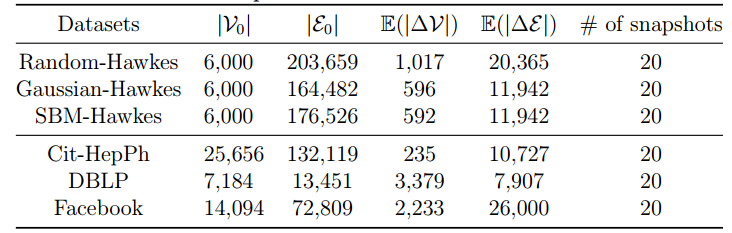
图 5 人工数据集和真实数据集的统计描述。
3.2 实验结果与分析
3.2.1 应用:动态图形实时监控和社区优化
在本应用中,我们旨在通过NAGA+AIUA和NSGA+AIUA的增量算法优化群落划分并监控相应的二维结构熵,以及基线TOA来实时量化动态图的每个快照的群落质量。具体来说,对于每个数据集,我们首先从Infomap、Louvain和Leiden中选择一种静态社区检测方法(简称静态方法)生成初始状态的社区划分。实验结果如图6(真实数据集)和图7(人工数据集)所示。
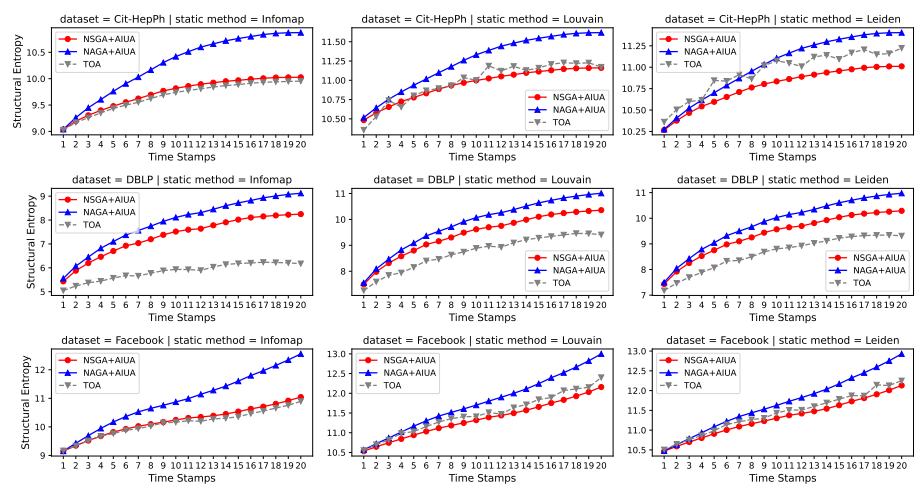
图 6 NAGA+AIUA、NSGA+AIUA和TOA在真实数据集上使用不同静态方法测量的更新后的结构熵。结构熵越低,性能越好。
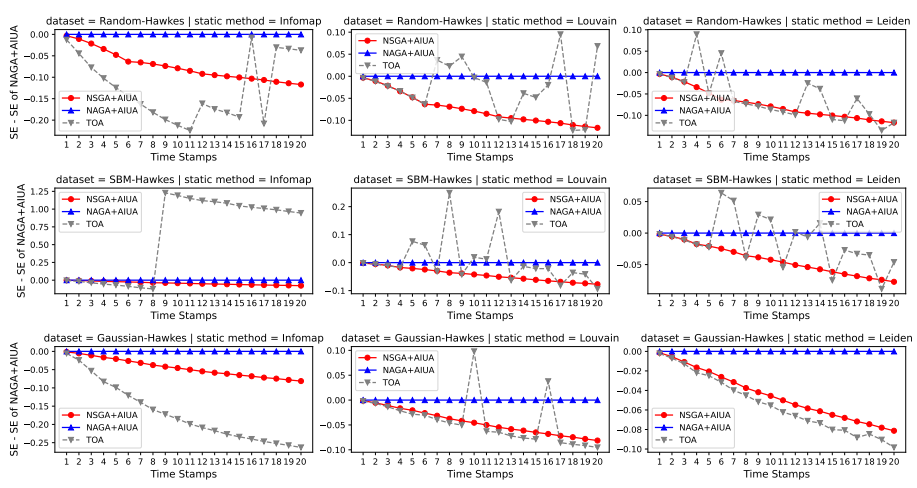
图 7 NAGA+AIUA、NSGA+AIUA和TOA在不同静态方法人工数据集上测量的更新结构熵。由于人工数据集的三条曲线比真实数据集的曲线更接近,因此所有显示的结构熵值都从NAGA+AIUA的结构熵值中减去,以更好地显示曲线之间的差异。
3.2.2 超参数研究
在这一部分中,作者评估了节点移位调整策略的不同迭代次数对更新结构熵的影响。作者使用迭代次数的NSGA+AIUA分别测量前一小节中每种情况下20个更新图的平均更新结构熵。实验结果如图8所示,更新的结构熵随着迭代次数的增加而减少。这是因为,随着迭代次数的增加,更多的节点将转移到它们的OPC,这导致结构熵进一步降低。实验还表明,节点转移调整策略具有良好的可解释性。
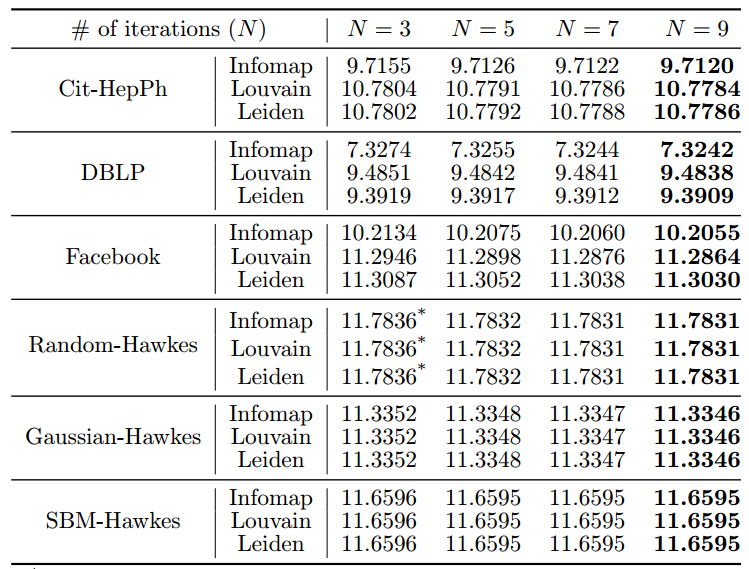
图 8 不同迭代次数下节点移位调整策略更新的结构熵。黑体数字表示最低结构熵。
3.2.3 时间消耗评估
图9给出了NAGA+AIUA和NSGA+AIUA(N=3,5,7,9)这两种增量算法在所有6个数据集上的耗时比较。图中的纵轴表示所选增量算法在所有20个快照中的平均耗时。横轴表示3个选定的静态方法。
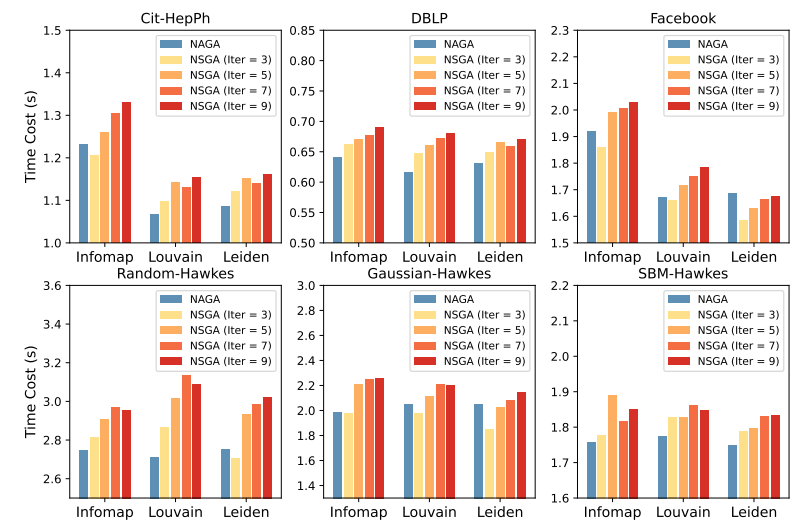
图 9 NAGA+AIUA和NSGA+AIUA (N=3,5,7,9)在不同静态方法下每个数据集超过20个时间戳上的平均耗时。
图10给出了在线算法NSGA+AIUA(N = 5)与离线算法TOA的时间对比。从结果可以看出,作者提出的所有增量算法都比现有的静态方法快得多。
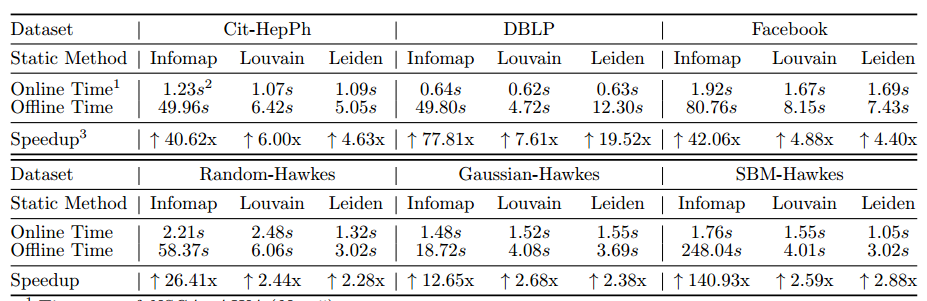
图 10 增量算法(在线时间)与基线传统离线算法(离线时间)的耗时比较。
3.2.4 Incre-2dSE与当前静态结构熵测量方法的差距
在这一部分中,作者研究Incre-2dSE与当前静态算法之间的差距。目前主流的结构熵测量静态算法称为结构熵最小化(SEM),是一种以结构熵为目标函数的静态图贪婪 k 维编码树构造算法。作者通过六个数据集上的所有时间戳测量了Incre-2dSE(NAGA/NSGA+AIUA)和2d-SEM的结构熵,如图11所示。
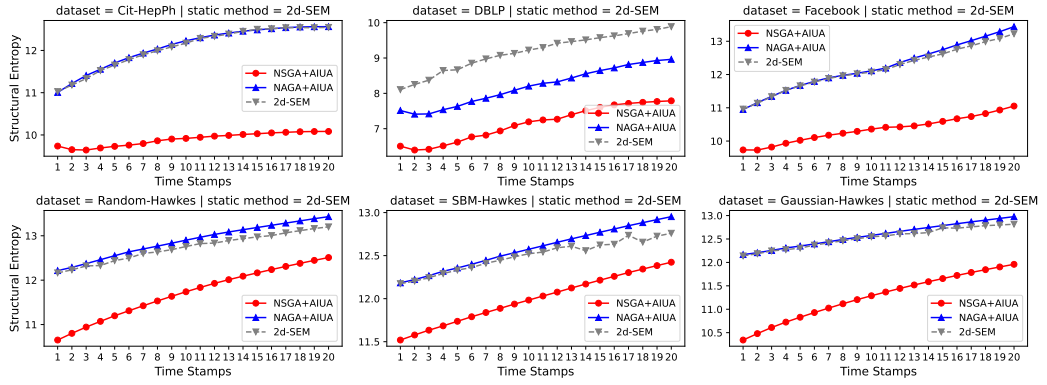
图 11 六个数据集上的时间戳测量Incre-2dSE(NAGA/NSGA+AIUA)和2d-SEM的结构熵。
3.2.5 有向加权图的一维结构熵测量
作者还评估了两种近似一维结构熵测量方法,即全局聚集和局部传播,在两个人工数据集上的时间消耗(ER数据集和Cycle数据集)。耗时实验结果如图12所示。
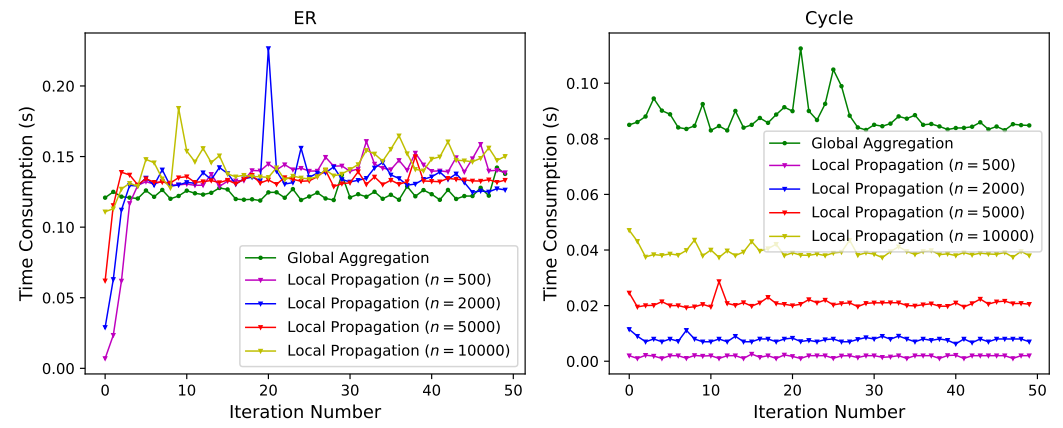
图 12 ER和Cycle数据集上全局聚合和局部传播的时间消耗。
除以上列出的实验结果之外,作者还进行了更新阈值分析、鲁棒性分析、收敛性分析。这些分析的结果表明,①设置更新的阈值可以提高效率,并更好地适应频繁更改的图形;②本算法使结构熵保持在一个稳定和较低的水平上,对不断增加的噪声具有很高的鲁棒性;③局部差值总是小于它的上界,有力地支持了局部差分及其一阶绝对矩的收敛性。
4 结论及展望
本文提出了两种新的动态调整策略,即朴素调整策略和节点转移调整策略,以分析更新的结构熵,并逐步调整原有的群落划分,使其朝着更低的结构熵方向发展。作者还实现了一个增量框架,即支持更新的二维结构熵的实时测量。进一步,作者讨论了提出的方法在加权图上的推广,以及在有向图和加权图上的一维结构熵计算。在未来,作者的目标是开发更多的动态调整策略,用于分层社区划分和高维结构熵的增量测量算法。
篇幅原因,我们在本文中省略了诸多细节,更多细节可以在论文中找到。感谢阅读!