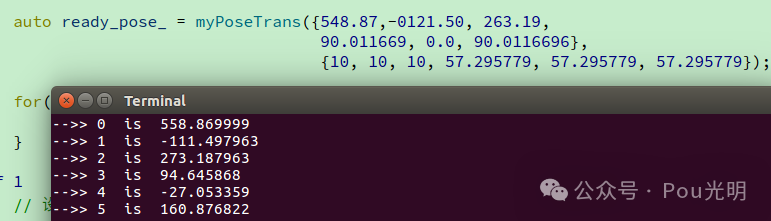
1、aubo arcs sdk poseTrans 使用例子
先贴代码:
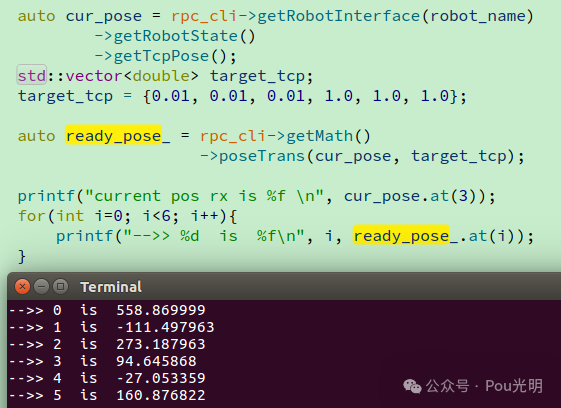
auto cur_pose = rpc_cli->getRobotInterface(robot_name) ->getRobotState() ->getTcpPose();std::vectortarget_pose;
target_pose = {0, 0, 0.0, 0, 0.0, 1.0};
auto ready_pose_ = rpc_cli->getMath()
->poseTrans(cur_pose, target_pose);
有了这部分代码,可以进一步说明与验证该接口。cur_pose是机械臂基于基坐标系的位置和姿态,毫米和弧度为单位,即p_from参数。对于target_pose参数,是对p_from进行的位置和姿态的变换,例子中target_pose表示位置不变,绕ry旋转1弧度。输出结果:
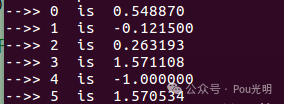
后面姿态表示是欧拉角,旋转方向是ZYX。绕Z轴旋转,但是变的是ry。OK,现在我们有了方程的参考答案,接下来自己推导解算过程。
2、借助Eigen库计算位姿变换
先整理下条件,已知当前机械臂的欧拉角姿态和位置,还已知变换的位姿。但从《机器人学导论》中学到的只有表示位姿的4×4的齐次位姿矩阵,所以需要欧拉角转旋转矩阵。
// 初始化欧拉角(rpy),对应绕x轴,绕y轴,绕z轴的旋转角度
Eigen::Vector3d euler_angle(pose_from.at(3) * DEG_TO_ARC,
pose_from.at(4) * DEG_TO_ARC,
pose_from.at(5) * DEG_TO_ARC);// 使用Eigen库将欧拉角转换为旋转矩阵 Eigen::Matrix3d rotation_matrix1; rotation_matrix1 = Eigen::AngleAxisd(euler_angle[2], Eigen::Vector3d::UnitZ()) * Eigen::AngleAxisd(euler_angle[1], Eigen::Vector3d::UnitY())* Eigen::AngleAxisd(euler_angle[0], Eigen::Vector3d::UnitX());</code></pre></div></div><p>上面转换也可以自己手写。</p><figure class=""><div class="rno-markdown-img-url" style="text-align:center"><div class="rno-markdown-img-url-inner" style="width:100%"><div style="width:100%"><img src="https://cdn.static.attains.cn/app/developer-bbs/upload/1723296822472982130.png" /></div></div></div></figure><p>将位置与旋转矩阵姿态构造成齐次矩阵:</p><div class="rno-markdown-code"><div class="rno-markdown-code-toolbar"><div class="rno-markdown-code-toolbar-info"><div class="rno-markdown-code-toolbar-item is-type"><span class="is-m-hidden">代码语言:</span>javascript</div></div><div class="rno-markdown-code-toolbar-opt"><div class="rno-markdown-code-toolbar-copy"><i class="icon-copy"></i><span class="is-m-hidden">复制</span></div></div></div><div class="developer-code-block"><pre class="prism-token token line-numbers language-javascript"><code class="language-javascript" style="margin-left:0"> Eigen::Matrix <double, </double,3, 4> m3x4_to; Eigen::Matrix <double, </double,4, 4> m4x4_to; Eigen::Matrix <double, </double,4, 4> m4x4_ret; m3x4_to << rotation_matrix1_to, pos_to; cout << "m3x4_to is :\n" << m3x4_to << std::endl;// np.concatenate((a,b)) m4x4_to << m3x4_to, homogeneous; m4x4_ret = m4x4*m4x4_to; cout << "m4x4_to is: \n" << m4x4_ret << std::endl; Eigen::Matrix <double, </double,3, 3> m3x3_ret = m4x4_ret.block(0, 0, 3, 3); cout << "m3x3_to ret is: \n" << m3x3_ret << std::endl; </code></pre></div></div><p>将旋转矩阵变为欧拉角便于观察:</p><div class="rno-markdown-code"><div class="rno-markdown-code-toolbar"><div class="rno-markdown-code-toolbar-info"><div class="rno-markdown-code-toolbar-item is-type"><span class="is-m-hidden">代码语言:</span>javascript</div></div><div class="rno-markdown-code-toolbar-opt"><div class="rno-markdown-code-toolbar-copy"><i class="icon-copy"></i><span class="is-m-hidden">复制</span></div></div></div><div class="developer-code-block"><pre class="prism-token token line-numbers language-javascript"><code class="language-javascript" style="margin-left:0">Eigen::Vector3d rotationMatrixToEulerAngles(Eigen::Matrix3d &R){
assert(isRotationMatirx(R));
double sy = sqrt(R(0,0) * R(0,0) + R(1,0) * R(1,0));
bool singular = sy < 1e-6;
double x, y, z;if (!singular){ x = atan2( R(2,1), R(2,2)); y = atan2(-R(2,0), sy); z = atan2( R(1,0), R(0,0)); }else{ x = atan2(-R(1,2), R(1,1)); y = atan2(-R(2,0), sy); z = 0; } return {x, y, z};
}
将上述组合,构建一个自己的myPoseTrans函数:
/**
@brief myPoseTrans
@param pose_from 起始位姿(空间向量)
@param pose_from_to 相对于起始位姿的姿态变化(空间向量)
@return 结果位姿 (空间向量)
*/
std::vectormyPoseTrans(const std::vector&pose_from,
const std::vector&pose_from_to)
{
std::vector pose;
// 初始化欧拉角(rpy),对应绕x轴,绕y轴,绕z轴的旋转角度
Eigen::Vector3d euler_angle(pose_from.at(3) * DEG_TO_ARC,
pose_from.at(4) * DEG_TO_ARC,
pose_from.at(5) * DEG_TO_ARC);
// 使用Eigen库将欧拉角转换为旋转矩阵
Eigen::Matrix3d rotation_matrix1;
rotation_matrix1 = Eigen::AngleAxisd(euler_angle[2], Eigen::Vector3d::UnitZ()) *
Eigen::AngleAxisd(euler_angle[1], Eigen::Vector3d::UnitY()) *
Eigen::AngleAxisd(euler_angle[0], Eigen::Vector3d::UnitX());Eigen::MatrixXd pos(3,1); pos(0,0)= pose_from.at(0); pos(1,0)= pose_from.at(1); pos(2,0)= pose_from.at(2); Eigen::MatrixXd homogeneous(1,4); homogeneous(0,0)=0; homogeneous(0,1)=0; homogeneous(0,2)=0; homogeneous(0,3)=1; Eigen::Matrix <double, </double,3, 4> m3x4; Eigen::Matrix <double, </double,4, 4> m4x4; m3x4 << rotation_matrix1, pos; cout << "m3x4 is :\n" << m3x4 << std::endl;// np.concatenate((a,b)) m4x4 << m3x4, homogeneous; cout << "m4x4 is: \n" < Eigen::MatrixXd pos_to(3,1); pos_to(0,0)= pose_from_to.at(0); pos_to(1,0)= pose_from_to.at(1); pos_to(2,0)= pose_from_to.at(2); // 转化为弧度 Eigen::Vector3d euler_angle_to(pose_from_to.at(3) * DEG_TO_ARC, pose_from_to.at(4) * DEG_TO_ARC, pose_from_to.at(5) * DEG_TO_ARC); // 使用Eigen库将欧拉角转换为旋转矩阵 Eigen::Matrix3d rotation_matrix1_to; rotation_matrix1_to = Eigen::AngleAxisd(euler_angle_to[2], Eigen::Vector3d::UnitZ()) * Eigen::AngleAxisd(euler_angle_to[1], Eigen::Vector3d::UnitY()) * Eigen::AngleAxisd(euler_angle_to[0], Eigen::Vector3d::UnitX()); Eigen::Matrix <double, </double,3, 4> m3x4_to; Eigen::Matrix <double, </double,4, 4> m4x4_to; Eigen::Matrix <double, </double,4, 4> m4x4_ret; m3x4_to << rotation_matrix1_to, pos_to; cout << "m3x4_to is :\n" << m3x4_to << std::endl;// np.concatenate((a,b)) m4x4_to << m3x4_to, homogeneous; m4x4_ret = m4x4*m4x4_to; cout << "m4x4_to is: \n" << m4x4_ret << std::endl; Eigen::Matrix <double, </double,3, 3> m3x3_ret = m4x4_ret.block(0, 0, 3, 3); cout << "m3x3_to ret is: \n" << m3x3_ret << std::endl; // 使用自定义函数将旋转矩阵转换为欧拉角 Eigen::Vector3d eulerAngle2 = rotationMatrixToEulerAngles(m3x3_ret); // roll,pitch,yaw cout << "roll_2 pitch_2 yaw_2 = " << eulerAngle2[0] << " " << eulerAngle2[1] << " " << eulerAngle2[2] << endl << endl; pose.push_back(m4x4_ret(0,3)); pose.push_back(m4x4_ret(1,3)); pose.push_back(m4x4_ret(2,3)); pose.push_back(eulerAngle2[0]*ARC_TO_DEG); pose.push_back(eulerAngle2[1]*ARC_TO_DEG); pose.push_back(eulerAngle2[2]*ARC_TO_DEG); return pose;
}
我的计算结果:
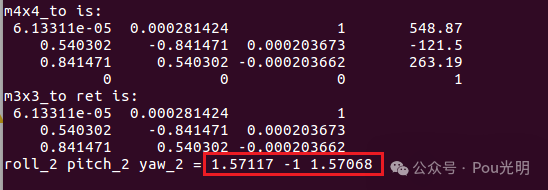
其他测试数据: