作者:韩冰, 张鑫云, 任爽
来源:《计算机研究与发展》
编辑:东岸因为@一点人工一点智能
3D传感器(如激光雷达和深度相机)的普及引起了人们对3D视觉的广泛关注,这些传感器采集的3D数据可以提供丰富的几何结构和尺度细节,这也在许多领域得到了实际应用,包括自动驾驶技术[1]、机器人控制技术[2]等。
3D数据通常可以用不同的格式来表示,包括深度图、网格、体素、点云、点云序列等[3],这些数据之间可以相互转换。在这些表示中,点云是最灵活的且最常用的,因为它们完整保留了物体在3D空间中最原始的几何信息,可以从以上3D传感器中直接获取或从各种3D建模软件中直接导出。然而,由于点云数据中各个点分布的不均衡性和表示的不规则性,处理点云仍然是一项有挑战性的任务。
近年来,深度学习技术逐渐成为各个领域的研究热点。PointNet[4]及其变体PointNet++[5]等方法的提出,解决了深度学习处理不规则数据格式的难题,也促使数据驱动的深度学习方法在点云上的研究不断地深入。
但由于PointNet[4]利用共享多层感知机(MLP)直接处理点云中的单个点,并通过最大池化(max pooling)操作来聚合各个点的所有信息,未能考虑点之间的相关性并进行充分利用,这也就导致了学习到的目标物体的特征存在着结构信息和局部细节的缺失。
卷积神经网络(CNN)作为一种标准的深度学习体系结构,由于其出色的局部信息聚合能力而被越来越多地采用,同时利用它的平移不变性和局部相关性,在机器视觉领域处理规则排列数据(如2D图像、视频)方面的研究中已经取得了一系列突破,极大地改进了几乎每项视觉任务的结果(如识别[6]、检测[7]、分类[8]、分割[9-10]等)。执行卷积运算的目的是从输入数据中提取出有用的特征进行学习。与深度神经网络(deep neural network, DNN)相比,卷积神经网络中的卷积运算减少了网络的训练参数量,提高了网络的泛化能力。因此,许多研究尝试将2D卷积网络直接扩展到3D空间,以使得卷积运算能够分析处理3D点云数据。
对比点云与图像之间的差异示例如图1所示。图像的像素(pixels)通常可以表示为规则的网格矩阵。在每个局部区域内,不同像素之间的相对位置是固定的,如图1(a)所示。而点云是3D空间中对目标物体进行曲面采样得到的一组点的集合,即P=\{p_i|i=1,2,...,n\} ,其中每个点p_i 默认包含1个位置信息,即3D坐标(XYZ),有时可能还包括颜色(RGB)信息或法线(normal)信息。
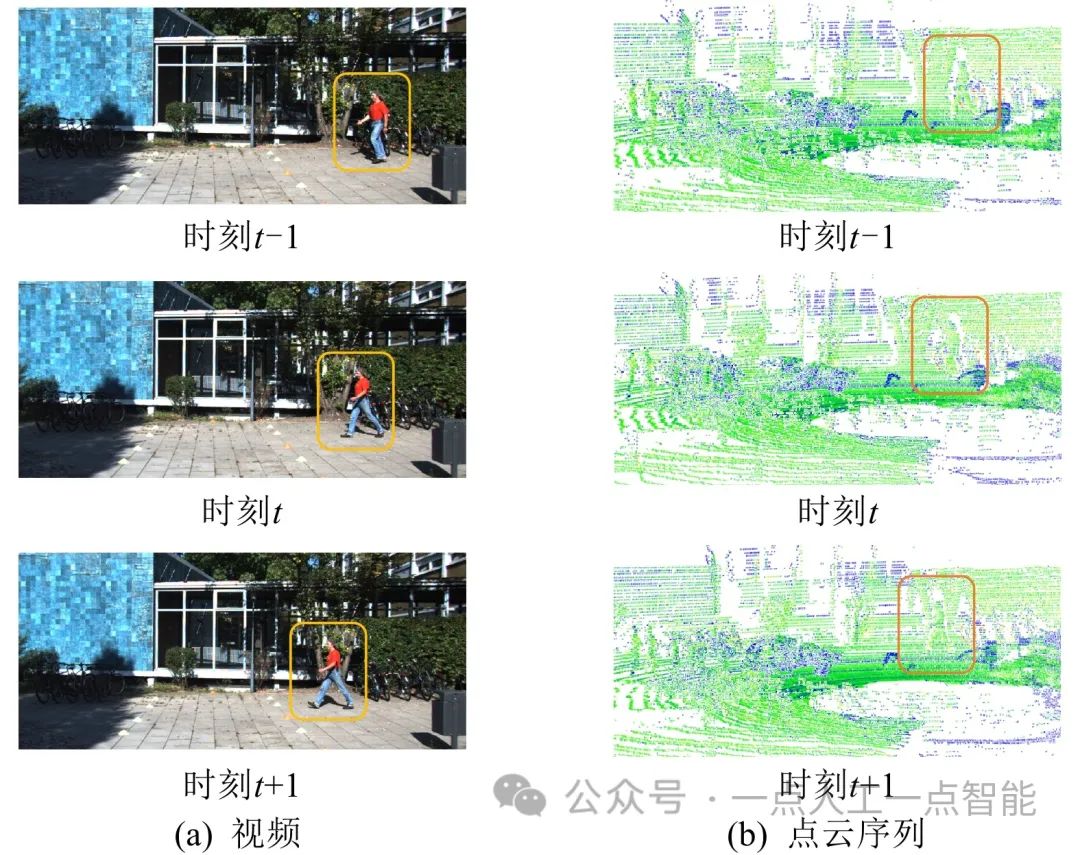
类似地,对比点云序列与视频之间的差异示例如图2所示。视频可以看作连续的多帧图像的集合,点云序列可以看作连续的多帧点云的集合。与图像相比,视频中增加了时序上下文关系(temporal context)。
将其推广到3D空间,与点云相比,点云序列中同样增加了时序上下文关系。因此,在进行以视频为输入数据的2D目标跟踪任务和以点云序列为输入数据的3D目标跟踪任务时,需要充分利用这一关系以处理连续帧之间的冗余,解决模糊失焦、部分遮挡等问题。
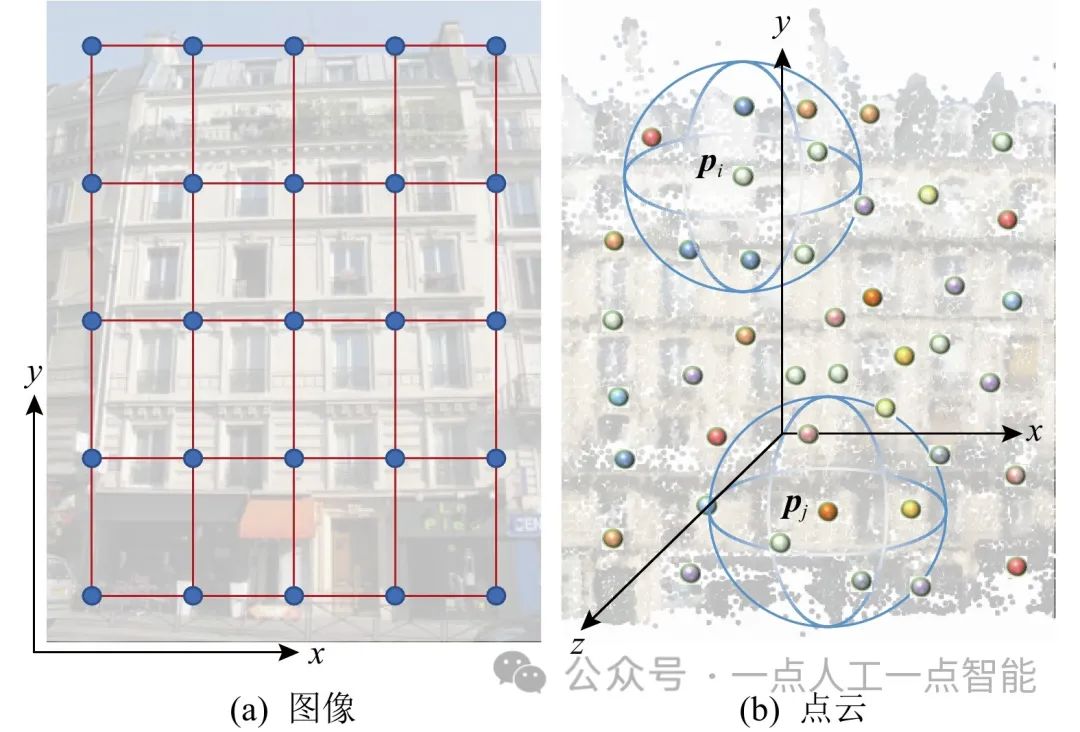
与图像/视频不同,点云更加灵活且无规则,点的坐标不一定位于固定网格上,即每个局部区域中所包含的不同点之间的相对位置都是不同的,如图1(b)所示,以p_i(x_i,y_i,z_i)\in \mathbb{R}^3 为中心的邻域和以 p_j(x_j,y_j,z_j)\in \mathbb{R}^3 为中心的邻域中各个近邻点的位置和个数是不同的,对应目标物体的形状也不同。因此,在图像/视频上使用的传统卷积运算不能直接应用于点云/点云序列。
综上所述,阻碍采用标准卷积运算学习3D点云特征的原因一般有3个:
1)点云是由无序的、不规则的点构成的集合,卷积运算应对点的输入顺序具有排列不变性(permutation invariance),即使输入点的顺序不同,学习之后也能得出相同的结果。
2)点云分布在3D几何空间中,卷积运算应对点云的刚性变换具有鲁棒性,包括旋转不变性(rotation invariance)、平移不变性(translation invariance)和尺度不变性(scale invariance)。
3)点云具有潜在的几何形状,卷积运算学习得到的点云形状应具备可区分性,防止丢失局部形状信息。
因此,针对这3方面的原因,为了学习3D点云的基本形状和几何结构,现有的研究主要分成了2种策略:一种策略是将3D点云转化为可以直接进行2D或3D标准卷积运算的结构;另一种策略是构造可以直接处理点云的卷积算子。首先,点云转化为其他结构的方法如图3所示,主要包括4个方法:
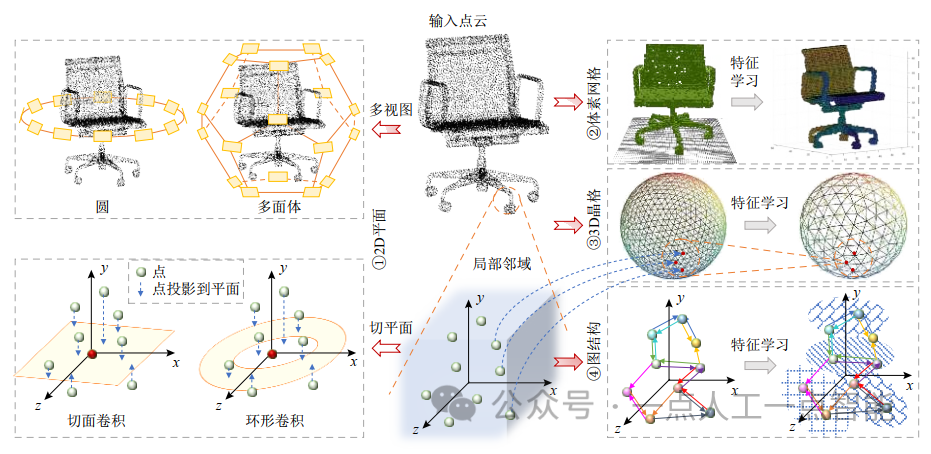
1)基于投影的方法(projection-based method)。如图3中的①所示,将3D点云投影到2D平面上,例如多视图[11-14]、切平面[15-17]。然而由于扫描设备生成的原始点云数据存在自遮挡(self-occlusion)或密度不均匀等问题,在投影过程中不可避免地会损失一些3D几何形状的深度信息和结构信息,同时在处理一些稀疏点云数据时通常效率低下且耗时。将点云投影为多视图还会因为不同视图之间的不连续性导致在细节敏感的任务(如部件分割)上的性能较差;将点云投影在切平面时依赖于对切平面的正确估计,此外还需要一些额外的辅助信息,即法线,然而许多像激光雷达等传感器生成的点云数据都不具备这样的信息。
2)基于体素的方法(voxel-based method)。如图3中的②所示,将物体的几何形式表示(如点云)体素化(voxelization)为最接近该物体的3D体素网格[11,18-24]。虽然这种方法易于实现,但由于点云分布的不均匀性,如何进行适当地体素化是关键。表示点云的体素与表示图像的像素类似,后者是像素点,而前者扩展到了立方体单元。这个立方体单元的大小与空间分辨率有关,体素网格划分越精细,立方体单元越小,空间分辨率越高,但计算复杂度和内存占用会随着细化程度呈立方级增长;反之,体素网格划分越粗糙,立方体单元越大,空间分辨率越低,计算复杂度和内存占用就越低,但分辨率不足会导致物体的一些局部细粒度几何细节的丢失,通常还会存在大量不包含点的空体素网格导致计算结果的偏差和内存空间的无效占用。
3)基于晶格的方法(lattice-based method)。如图3中的③所示,将点云投影到规则的晶格空间,例如正多面体晶格(permutohedral lattice)[25]、球形晶格(spherical lattice)[26]。这种方法可以解决点云的部分位置稀疏性问题,但类似于体素网格,通常也需要消耗大量内存来存储晶格特征,且在高分辨率要求下计算复杂度将会大大增加。其次,投影到某个规则晶格空间中,很有可能不再保留这些点之前在原始欧氏空间中所具备的几何信息。
4)基于图的方法(graph-based method)。如图3中的④所示,将3D点云构造为图结构,点云中的各个点作为图的顶点,点与其邻域内的部分近邻点形成有向边,进而借助于图卷积网络(GCN),在谱域(spectral domain)[27-31]或空间域(spatial domain)[32-43]中学习特征。这些方法能够直接处理不规则的数据结构,但也存在一些缺点,例如,局部图的构造不是稀疏不变的。从同一物体表面采样的不同密度点云会得到不同的邻域,从而可能产生不同的图构造结果。同时,在构建邻域时,可能会忽略法线方向,从而导致局部几何信息的丢失。这些对不规则输入数据的转化方法均会在一定程度上导致物体的几何信息的丢失,并且这些转化操作会导致计算复杂度和内存消耗的急剧增加。
鉴于此,越来越多的研究人员致力于研究基于点的方法(point-based method),构造各种各样的卷积运算及卷积网络来学习点及其邻域内的其他点的特征,直接在原始点云数据上进行分析,可以在处理不规则的点云任务上实现优异的性能。为了能够充分利用数据的空间局部相关性,卷积运算中使用的卷积算子也成为了提高点云分析的算法性能和结果准确性的重要影响因素。因此本文重点关注点卷积算子(point convolution operator)及其对应的网络结构,这类卷积运算可以直接处理原始点云,而不进行任何转化,不需要任何中间表示,也因此不会引入其他的信息损失。
目前国内外关于点云的相关综述有很多,文献[3]涵盖了不同的应用,按照形状分类、目标检测与跟踪、点云分割3大任务进行划分,对应用在点云的深度学习方法的最新进展进行了全面综述和详细展开,涉及的方面较为广泛。
文献[44]将现有的点云特征学习方法分为基于点的特征学习和基于树的特征学习,并通过具体任务的应用来分析这些方法的优缺点。文献[45]通过分析点云应用中面临的挑战和深度学习的优势,详细展开分析了几种经典的直接处理点云的深度学习方法。文献[46]系统回顾并详细介绍了自动驾驶应用领域中的激光雷达点云的特定任务。
此外,还有一些综述侧重于对点云的具体任务的基础原理及关键技术进行分类、分析与总结,例如,点云法向量估计任务[47]、点云场景分割任务[48]、点云语义分割任务[49-51]、点云配准任务[52]、点云序列的点态预测任务[53]等。
01 标准卷积
卷积神经网络,最早是由LeCun等人[6]提出并应用在手写字体识别与分类任务中,称为LeNet-5。在过去的几年中,2D卷积的应用最为广泛且研究相对成熟,最大的原因是图像的规则像素可以很容易地通过权重共享(weight sharing)和平移不变(translation invariance)特性进行相应的卷积运算。此外,还可以通过改变卷积核的构造,如空洞卷积(dilated/atrous convolution)、可分离卷积(separable convolution)、组卷积(group convolution)等,使得卷积网络能够根据多尺度层次结构上的感受野(receptive field)来学习和丰富特征。与2D卷积不同,3D卷积在问题上并没有达到相同水平的研究进展,这是由于其在建模和训练中存在着一些障碍,如计算复杂度较高;内存占用较大;存在大量待学习参数,容易产生过拟合,因此需要对网络架构或卷积运算进行改进来提升特征学习能力。
本节将回顾这些标准卷积运算的原理,以帮助理解与第2节的点云卷积运算之间的区别与联系,为后续各种处理不规则3D点云数据的卷积运算的深入研究奠定基础。
标准卷积运算是指卷积算子以滑动窗口的方式在局部区域上的点集合或者特征集合进行加权求和得到输出结果的过程,这一过程能够从若干相关特征中以特定的方式提取新的特征。卷积实际上是一种积分运算,相应的离散卷积和连续卷积的一般定义分别为:
1)离散卷积(卷积算子定义在离散空间)。
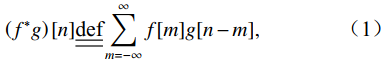
其中卷积算子\text{g}:\mathbb{S}\rightarrow \mathbb{R} 和特征f:G\rightarrow \mathbb{R} 分别是定义域S=\mathcal{Z}^D 和G=\mathcal{Z}^D 上的函数。
2)连续卷积(卷积算子定义在连续空间)。

其中卷积算子\text{g}:\mathbb{S}\rightarrow \mathbb{R} 和特征f:G\rightarrow \mathbb{R} 分别是定义域S=\mathbb{R}^D 和G=\mathbb{R}^D 上的连续函数。
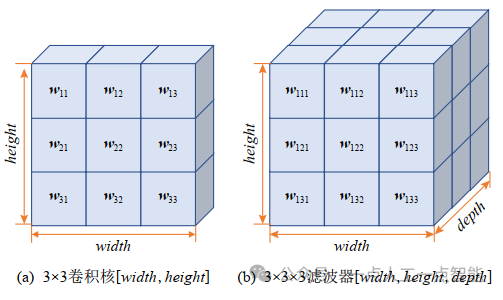
2D卷积运算是指卷积算子即如图4(a)所示尺寸为[width, height]的卷积核(kernel)在宽度和高度2个维度上的滑动并计算,此时D=2。而3D卷积是指卷积算子即如图4(b)所示尺寸为[width, height, depth]的滤波器在宽度、高度、深度的3个维度上的滑动并计算,此时D=3。
02 基于点的卷积
标准卷积网络的成功应用表明,保持卷积运算的稳定性是必不可少的,即邻域大小不变和邻居个数不变。然而由于点云中的点排列不规则、点密度不均匀,这种稳定性属性在点云数据中是不存在的,无法始终同时保持区域大小不变(例如,半径为R的局部邻域)和邻居个数不变(例如,K个近邻点)。这使得标准卷积难以处理此类数据。
为了克服这一问题,越来越多研究人员致力于提出有效的直接作用于点云的卷积算子,如图4所示,这些算子大多是即插即用(plug-and-play, PnP)的,可以很容易地集成到各种3D点云分析任务(如分类、分割)的流程(pipeline)中去,详见第3节。因此,可以总结出利用卷积网络在点云上进行有效学习主要有3个关键要求:
1)定义输入点集,该点集可以是整个点云的集合,也可以是点云的子集。前者需要描述整个点云的全局特征向量;后者为每个点集寻找一个局部特征向量,在学习全局特征时可以进一步组合。
2)构造一个能够在点云上使用的卷积算子,该算子能够有效解决点云的排列不变性和密度不均匀性,并且可以学习点之间的局部几何特征。
3)构造一个能够集成卷积算子的卷积神经网络,该网络结构可以从输入点云中逐步提取局部(local)到全局(global)的深层次语义信息,辅助点云任务更好地完成。
首先,类似于标准卷积,可以将基于点p_i\in\mathbb{R}^D 的卷积定义为

其中\odot 是特征函数f:\mathbb{R}^D\rightarrow\mathbb{R}^F 和权重函数\text{g}:\mathbb{R}^D\rightarrow\mathbb{R}^F 之间的哈达玛积(Hadamard product),特征函数f 是为每个绝对位置p_j\in\mathbb{R}^D 分配一个特征向量f(p_j)\in \mathbb{R}^F ,权重函数\text{g} 是为每个相对位置p_i-p_j\in \mathbb{R}^D 映射一个权重向量\text{g}(p_i-p_j)\in \mathbb{R}^F 。使用蒙特卡洛积分(Monte Carlo integration),可以进一步将卷积运算近似为对含有N 个点的点云操作
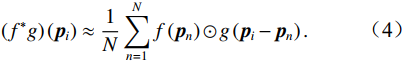
为了更准确有效地提取高维特征和局部细粒度信息,在2D图像卷积中,通过如图4(a)所示的3×3或5×5的像素核来定义局部邻域范围。类似地,对于点卷积,通过在每个点周围定义局部邻域和近邻点集合来实现
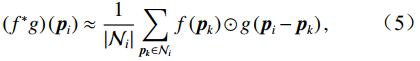
其中\mathcal{N}_t 是点p_i 的局部邻域内的近邻点集,p_k 是p_i 的第k 个近邻点。这也就满足了关键要求1)。
其次,针对关键要求2),点云卷积性能取决于卷积算子中权重函数w 的学习和更新。因此,可以根据权重函数的类型,将现有的基于点云的卷积方法分为离散卷积和连续卷积,如图5所示。离散卷积方法中的卷积权重与近邻点和中心点之间的偏移量(相对位置)有关,通常根据距离等特征为落入同一个局部区域的所有点分配相应的权重。而连续卷积方法中的卷积权重与近邻点相对于中心点的空间分布有关,通常根据近邻点的空间分布为每个点分配权重。

显然,在进行卷积之前,大多研究都会首先采样得到中心点集,然后寻找每个中心点的局部邻域及其近邻点集\mathcal{N}_t 。目前使用最广泛的采样中心点的方法主要有随机点采样(random point sampling, RPS)、最远点采样(farthest point sampling, FPS),后者相对于前者的优势在于它可以尽可能地覆盖空间中的所有点,找到一些有代表的点,而前者的时间复杂度相对较低[54]。
关于寻找某个点的局部邻域的策略,目前在点云研究中使用最广泛的除了图5(a)所示的球查询(ball query)算法外,还有K近邻(K nearest neighbor, KNN)算法,二者的区别是前者指定邻域范围,选择在以中心点为球心、以R为半径的球形区域内的点作为该中心点的近邻点,组成的集合即为\mathcal{N}_t ;而后者指定近邻点数,寻找与中心点距离最近的K个点作为该中心点的近邻点。有研究表明二者的选择对实际点云任务的性能影响相差不大[40]。
在之后的小节中,我们的重点是分析各研究工作所提出的卷积算子的设计原理及在此基础上构建的卷积网络。因此若研究工作中没有涉及对点邻域进行改进,则默认前提是通过球查询算法和KNN算法采样得到的中心点及其近邻点集。
2.1 离散卷积
在不规则点云上进行卷积运算的一个首要问题是,权重向量的空间位置通常与输入点无法对齐。将点云体素化为规则网格解决了这一问题,但代价是丢失了局部几何结构,这对于一些追求高性能的点云任务通常是不可取的。因此,在基于点的离散卷积中,一些研究首先想到通过解决点的排列不变性问题来处理这一问题,还有一些研究考虑了点的空间几何特性。
2.1.1 排列不变性
为了解决点云的排列不变性,Hua等人[55]通过指定点的输入顺序,提出了逐点卷积算子(pointwise convolution)。
具体来说,将所有点按照指定顺序(如3D坐标x→y→z)依次输入到逐点卷积神经网络(pointwise CNN)中,以每个点为中心得到指定数量的近邻点并将其划分到对应的核单元(kernel cell),每个核单元内的所有点都具有相同的核权重,核的尺寸可以根据每个卷积层中不同数量的近邻点进行适当地调整。
类似地,Li等人[56]提出了一个\mathcal{X}-Conv 卷积算子,关键在于将局部坐标系的原点定位在每个中心点,使得该算子不依赖于中心点及其近邻点的绝对位置,而依赖于它们的相对位置,采用多层感知机根据相对位置学习一个\mathcal{X}- 变换矩阵作为卷积核权重矩阵,与中心点特征及其近邻点特征的结合矩阵进行卷积运算得到高维特征,将多个\mathcal{X}-Conv 进行级联(concatenation)或跨层连接(skip connection)可以得到点卷积神经网络(PointCNN)的多种结构从而来进行不同的点云任务。
由于在一些实际场景中,物体的大小各不相同,为了使提取的特征适应不同大小的物体,即小物体具有较小范围的邻域特征,大物体具有较大范围的邻域特征,基于卷积算子\mathcal{X}-Conv 和网络PointCNN[56],Zhang等人[57]提出了基于彩色植被指数的多尺度卷积神经网络(MCCNN),利用颜色信息为原始点云数据中的每个点计算超绿(excess green, ExG)和超红(excess red, ExR)这2种彩色植被指数,并与其位置信息一起作为输入特征,然后设置中心点的不同数量的近邻点或者不同范围的邻域,得到不同的卷积核来提取多尺度特征,同时增强点云的可区分性。
2.1.2 点几何特性
将点从欧氏空间映射到了其他空间,虽然解决了点云的排列不变性问题,但也因此损失了3D物体的几何信息。因此,为了在整个特征提取中保留欧氏空间的几何结构信息,一些研究通过4种方法来更充分地学习点之间的几何信息,提升网络的学习效率及性能,包括:建立点的方向向量;设计点的局部邻域;改变点卷积的感受野;构建点与卷积权重的相关性。
1)建立点的方向向量[58-59]
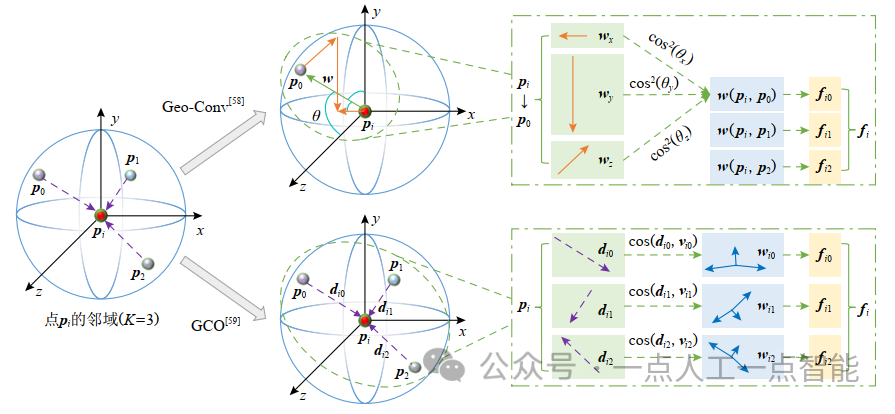
Lan等人[58]基于物体的几何信息隐含在点云的坐标中这一合理的假设,提出了一种几何卷积算子(geometric-induced convolution, Geo-Conv),如图6所示,具体卷积运算过程包括:
①特征分解(feature decomposition)。将中心点与其近邻点所组成的边向量分解到3个正交坐标基上,沿着各个基底(base)独立学习边特征。
②特征提取(feature extraction)。对中心点来说,通过与一个可学习的方向相关权重矩阵进行加权求和来提取该点在各个方向上的特征。
③特征聚合(feature aggregation)。将提取到的特征与边向量和正交基之间的夹角成比例地聚合得到点之间的几何结构信息。
通过逐层扩大卷积的感受野,将多个Geo-Convs作用于不断增大的局部邻域以分层提取特征,构建一个几何诱导卷积神经网络(geometric-induced CNN, Geo-CNN),对局部区域点之间的几何结构进行建模,最后通过一个最大池化层来聚集所有点的全局特征。然而网络在每次卷积都需要重新计算所有点的近邻点,使得其计算复杂度大大增加,不适合处理大规模场景。
此外,除了物体内部点的几何特征,边界信息在一些点云分割任务中起着重要作用,当边界信息被忽略时,提取的特征通常是模糊的,因为它们混合了边界邻域内属于不同类别的点的特征。
随着网络的深入,如果其他点包含边界点的特征,那么边界上的这些模糊特征将不可避免地分层传播到更多点,导致不同物体的信息跨边界传播,不同物体之间的过渡区域被错误分割。
为了解决这一问题,Gong等人[59]首先提出了一个边界预测模块(boundary prediction module, BPM)预测边界点;基于预测的边界,设计了一个边界感知几何编码模块(boundary-aware geometric encoding module, GEM)对几何信息进行编码,使同一个邻域内不同类别的局部特征不会相互影响;此外为了使得提取的特征更具区分性,还提出了一种轻量级几何卷积运算(geometric convolution operation, GCO),通过几何卷积核(geometric kernel)和邻域内点的方向向量构成的矩阵相乘得到中心点的特征,在一个包含K个近邻点的邻域中,其几何结构可用K个3D方向向量表示。如图7所示,K=3时,构造的几何卷积核是一个具有3个方向向量的矩阵,每个向量表示3D空间中的1个方向,这3个方向向量和中心点可以表示一个四面体(最简单的多面体),因此卷积核本身可以描述点在方向上的分布。
2)设计点的局部邻域[60-61]
尽管采用球查询和K近邻的点邻域搜索方式是直观的、简单的,但由于邻域范围R或近邻点数K是预定义的,这也就限制了中心点的局部邻域大小,同时该值设置的不合理也会导致网络的性能变差。
相比于图7(a)中通过球查询得到的球形区域(ball),Zhang等人[60]提出了一种壳卷积算子(ShellConv),将中心点的3D球形邻域划分为多个壳形区域(shells),即同心球壳(concentric spherical shell),一个shell表示2个相同球心不同半径的球面之间的空间范围,如图7(b)所示,同时构建包含多个ShellConvs的壳卷积神经网络(ShellNet),将中心点的K个近邻点按照到中心点的距离升序排列并划分到不同的壳内;同一个壳内的点,通过全连接层和最大池化层计算出一个局部特征,最后根据多个壳的局部特征加权求和得到中心点的聚合特征,提高了局部特征的学习效率。
Lei等人[61]定义了一个球卷积(spherical convolution)算子,利用空间分区将中心点的球形邻域划分为多个大小不一的箱形区域(bins),如图7(c)所示,并为每个bin定义一个可学习权重矩阵,该矩阵对位于该子区域内的近邻点进行加权求和得到卷积结果。
与标准卷积核相比,后者必须保持所有区域大小统一,并依靠提升分辨率来提取更细粒度的特征,这通常会导致较高的内存占用问题,而球卷积算子的多尺度区域解决了这一问题,使得卷积运算更加灵活,不仅能够对相同区域特征实现权重共享,也有效学习了具有非对称性的几何特征。基于球卷积算子,还提出了八叉树(octree)[62]引导卷积神经网络(octree guided CNN, Ψ-CNN),该网络具有与八叉树深度相同数量的卷积层,根据八叉树的数据结构对输入点云进行空间划分,分层下采样得到中心点并构造点邻域。
随后,由于球卷积算子的灵活性和优越性,Lei等人[43]又将其扩展到图卷积网络中提出了SPH3D-GCN,此外,考虑到划分边界和密度分布的影响,将模糊机制(fuzzy mechanism)引入到该卷积算子中,提出了模糊核(fuzzy kernel),并在此基础上构建了一个高效的适用于点云分割任务的图卷积网络SegGCN[42]。

3)改变点卷积的感受野[63-66]
与2D图像卷积运算类似,在3D点云中,决定卷积神经网络某层的输出结果中1个特征所对应的输入层的区域被称作感受野,其大小直接关系到网络处理各种任务的性能。
因此,增加感受野大小的常用方法有2种:一种方法是堆叠多个(点)卷积层,在提升网络性能的同时也引入了更多的参数,增加了计算复杂度,导致额外的内存消耗;另一种方法是增大卷积核的尺寸,参考如图8(a)和图8(b)所示的1D和2D空洞卷积原理,在扩大感受野的同时可以不损失信息,得到了如图8(c)所示的3D空洞卷积算子[63-64]。
Pan等人[63]提出的点空洞卷积算子(point atrous convolution, PAC),通过设置不同的采样率r在特征空间或度量空间中对中心点的近邻点特征进行稀疏采样(sparse sampling)。特别地,如果采样率为r=1,则PAC将退化为EdgeConv[39]。这样,在不增加参数量和计算量的前提下,通过增大采样率就可以有效地扩大卷积的感受野。
同样,类似于2D空洞空间金字塔池化(atrous spatial pyramid pooling, ASPP)[10]的原理,将不同空洞率的空洞卷积平行或者级联堆叠来获取多尺度信息,由此提出了点空洞空间金字塔池化(PASPP),得到不同采样率下的近邻点特征来聚合中心点的多尺度局部特征。最后,集成多个PACs和PASPPs,构建了相应的具有排列不变性的点空洞卷积网络(PAN),充分利用局部几何细节进行点云分析。
类似地,Engelmann等人[64]首先对比了不同尺度感受野对网络性能的影响,然后提出了一种空洞点卷积(DPC)算子集成邻近点的特征,通过设置不同的空洞因子d改进原先的K近邻,扩大中心点的局部邻域范围,搜索K×d个近邻点并仅保留排序后的每K个近邻点集中的第d个点来学习核权重。
特别地,如果r=1,则DPC将退化为使用K近邻寻找近邻点的Pointwise Convolution[55]。原先通过简单地增加近邻点数来提高网络性能的方法会增加计算成本,从而导致推理时间变慢,而引入d后增加了点卷积的感受野大小,在几乎不增加额外计算成本的情况下显著提高性能。

鉴于以往的研究工作大多只关注空间维度上的特征提取,而忽略了通道维度,使得点云的特征学习不充分,因此类比于2D可分离卷积,Cui等人[65]提出了一种轻量级注意力模块(LAM),它采用了深度可分离卷积(DSConv)算子在不降低网络性能的前提下提高计算效率,同时采用基于通道统计特征的注意力机制(attention mechanism)通过自动缩放不同特征通道的权重来提高网络精度。
DSConv将作用在点云上的卷积运算分为2个步骤,减少特征提取在空间和通道2个不同维度上的相互干扰:①深度卷积(depthwise convolution)。在输入的每个特征通道上单独执行空间卷积;②点卷积(pointwise convolution[55])。使用1×1卷积将特征通道映射到新的通道空间,选择不同的卷积核进行这2个维度的卷积。
为了解决3D旋转,即SO(3)、3D变换,即SE(3)①的等变性和不变性,Chen等人[66]提出了一种用于点云的SE(3)可分离卷积(separable convolution, SPConv)算子,首先,将卷积分解为1个SE(3)点卷积算子和1个SE(3)组卷积算子,分别在3D欧氏空间和SO(3)空间中交替进行卷积运算,使用SE(3)空间中定义的特征作为输入并输出每个点的SE(3)等变特征。SE(3)可分离卷积在不影响性能情况下显著降低了SE(3)卷积的计算成本。其次,将注意力机制与全局池化相结合提出了一个组注意力池化(group attentive pooling, GAP)操作,进行从等变特征到不变特征的转换②。最后,集成卷积和池化构建了一个SE(3)等变点网络(equivariant point network, EPN)作为通用框架,可以根据下游任务生成等变或不变的点特征。
4)构建点与卷积权重的相关性[67-69]
考虑到注意力机制在提取全局特征上的优越性,为了帮助卷积得到更细粒度的特征,Dang等人[67]提出了邻域注意力卷积(neighborhood attention convolution, NAC),在不同的近邻点上自适应地进行特征选择,充分挖掘每个局部区域内的细粒度局部几何特征,通过融合中心点与近邻点的相对位置、绝对位置和高维非局部点特征来获得邻域注意力系数。使用Softmax函数将所有近邻点的邻域注意力系数归一化到范围(0, 1)来表示不同近邻点的重要性。然后,基于NAC并结合2D组卷积的原理,又提出了分层交错组卷积(HIGConv),包含第1阶段分层组卷积(PHGC)和第2阶段分层组卷积(SHGC)。
具体来说,PHGC将NAC的输入特征和参数划分为多个分区,为了便于不同分区之间不同级别的特征映射的交互,将相邻2个分区的特征在通道维度上进行融合作为下一个分区的输入特征,以扩大输出特征维度、增强学习能力。最后,连接所有分区的输出特征并在特征通道维度上进行洗牌(shuffle),以充分融合所有分区的特征,提取细粒度的局部几何特征。
类似地,SHGC通过将多层感知机的输入特征和参数划分为多个分区并在通道维度上进行洗牌后提取得到可区分的非局部点特征,这样丰富的局部到全局形状信息可以通过2部分的输出特征聚合在一起。然后,构建包含多个HIGConvs的分层交错组卷积神经网络(HIGCNN),其核心是多尺度关系(multi-scale relation, MSR)模块,用于集成不同尺度区域之间的关系,对多尺度细粒度特征进行编码,将2个区域的局部几何特征融合为关系描述符,通过Softmax函数将其归一化到范围(0, 1)内生成区域之间的关系分数,用于自适应地增强有用的结构特征,抑制无用的噪声特征,从而以较少的冗余参数和较低的计算成本获得足够的特征表示能力。
此外,Mao等人[68]提出了一种插值卷积(InterpConv)算子来度量输入点云与卷积权重之间的几何关系。在每个权重向量附近找到一组输入点,然后对它们的特征进行插值以分配给权重矩阵进行卷积运算。
由此提出了2种插值函数:三线性插值(trilinear interpolation)和高斯插值(gaussian interpolation)。它们的权重计算方法不同,三线性插值通过计算相对于中心点的8个晶格点的权重坐标,然后使用这些权重将输入点特征反向分配给相邻的权重坐标,再进行加权求和得到中心点的新特征。而高斯插值是使用高斯函数来计算权重。
其他函数,如线性基函数(linear basis functions),也可以用作插值函数。级联多层多感受野的InterpConvs以构建插值卷积神经网络(InterpCNN),解决点云的排列不变性,且对点云密度不敏感,但其存在的一个缺点是预先指定的插值函数无法适应点云的变化,导致其鲁棒性较差。
在特征提取过程中,需要进行逐步下采样来减少点的数量,增加特征维度。为了在这一过程中不丢失点云的几何形状信息,Nguyen等人[69]提出了一种统计卷积(statistical convolution, StatsConv)算子,利用统计学中的样本矩,结合基于从点云中提取的不同矩的全局特征和输入点进行非线性变换后的逐点特征,通过几个非线性全连接层投影到一个新的特征空间;封装了全局特征和局部特征,用于提取各种统计信息来表征输入点集的分布信息。
2.2 连续卷积
连续卷积方法是在连续的空间中定义卷积算子,其中近邻点的权重与中心点的空间分布有关。连续卷积运算最重要的部分是特征建模的方式。考虑到实际任务的复杂性,卷积核函数也可能是极其复杂的,因此主要有2种策略:一种策略是增加一些虚拟化的辅助信息;另一种策略是对所使用的卷积核函数进行参数化。
2.2.1 虚拟化辅助信息
为了保留3D点坐标编码的全局信息,一些研究工作通过增加或者设计一些虚拟点[70-72]、虚拟空间[73-74]、虚拟结构[75-76]来辅助进行卷积运算,如图9所示。
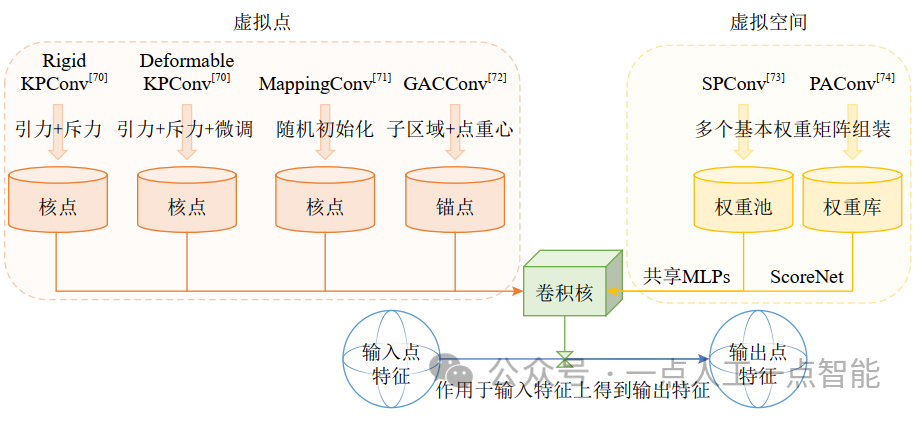
1)虚拟点
首先,Thomas等人[70]引入了核点(kernel points)并提出了一种核点卷积(KPConv)算子,在中心点的球形邻域内确定一组任意数量的核点集合,每个核点带有一个可学习的权重矩阵,相关系数取决于任意点与核点的相对位置(欧氏距离)。
通过分别计算邻域内的所有近邻点与核点的权重矩阵的乘积对该点进行特征变换,最后累加所有近邻点的特征得到中心点的特征。由此可见,核点位置对卷积算子至关重要,因此通过解决一个球形空间中最佳覆盖的优化问题来计算核点位置,并进一步提出了处理简单任务的刚性卷积(rigid KPConv)算子和处理复杂任务的可变形卷积(deformable KPConv)算子。对于刚性卷积,球心(中心点)作为一个核点;球心对其他核点有一定的引力(attractive force)来吸引它们靠拢;其他核点之间有一定的斥力(repulsive force)来使它们相互远离。这个由引力、斥力组成的系统稳定后,即可确定每个核点位置。
对于可变性卷积,按引力、斥力的方法确定出来的所有核点的位置可能不是最优的,因此通过计算核点相对于原始位置的偏移量来优化或微调每个核点的位置。在此基础上,还构建了含有多个KPConvs的分类网络(KP-CNN)和分割网络(KP-FCNN),每个卷积层采用下采样以在不同密度的点云下实现高鲁棒性。同样,Yan等人[71]也引入了核点并提出了一种映射卷积(mapping convolution, MappingConv)算子,不同的是MappingConv中的核点位置最初是在以中心点为球心的单位球形邻域中随机初始化生成的,根据3个多层感知机学习到的映射函数,基于近邻点和核点之间的空间位置关系(欧氏距离)将不规则的近邻点特征映射到一系列可学习的核点上,然后通过反向传播以数据驱动的方式对核点位置进行更新。最后将学习到的权重应用于位于核点上的聚合特征集合得到卷积结果。
类似地,Zhang等人[72]引入了锚点(anchor points)并提出了一种全局上下文感知卷积(GCAConv)算子。为每个中心点生成一组锚点集合来近似表征全局输入形状特征。这里的锚点位置对卷积算子同样至关重要,因此以中心点为原点构造一个全局加权局部参考系(LRF),通过投影将近邻点的3D全局坐标转换为局部坐标,根据LRF将该中心点的局部邻域划分出8个细分邻域子空间,将每个邻域子空间中近邻点的重心作为锚点,通过1D卷积编码局部点集和全局锚点之间的局部和全局关系(local-global relation)来定义卷积权重,执行卷积以提取局部和全局特征(local-global feature)。
2)虚拟空间
首先,Yang等人[73]定义了一个可学习的卷积权重池(weight pool),并提出了一种空间探测卷积(SPConv)算子。首先采用一个几何引导的索引映射函数(index-mapping function),将中心点与近邻点之间的几何特征转换为权重索引,学习自适应地将3D空间划分为多个子空间以进行局部几何结构识别。然后从权重池中为每个子空间中的点分配一个共享的权重矩阵;将每个近邻点的几何特征输入到共享多层感知机中,输出的特征映射被视为每个子空间所属的等级。最后与相应的权重进行卷积和聚合,以获得更深层次的语义特征。
类似地,Xu等人[74]定义了一个可学习的卷积权重库(weight bank),并提出了一种位置自适应卷积( PAConv)算子和一个分数网络(ScoreNet),将中心点及其近邻点之间的相对位置关系向量输入到网络中以自适应学习对应的归一化在(0, 1)范围内的系数向量,根据向量中的概率值组合权重矩阵,值越高表示位置向量和权重矩阵之间的关系越强。通过组合存储在权重库中的基本权重矩阵与网络预测出的位置自适应系数来构造动态卷积核函数用于卷积运算。
这2项工作都是通过建模点之间的位置关系来提取几何空间特征,但存在的问题是存储过多的权重矩阵可能会造成网络冗余,带来较大的内存占用和计算负担,因此选择合适的权重矩阵是决定二者网络性能的关键。
3)虚拟结构
为了加快计算速度,Groh等人[75]提出了一个卷积算子Flex-Convolution,将卷积核的权重定义为中心点的局部邻域上的标准标量积,并与其K个近邻点的特征向量进行卷积运算,网络还集成了采用类似方法的最大池化Flex-Max-Pooling进行聚合操作,使用较少的参数和较低的内存消耗得到了极具竞争力的性能。随后,Boulch[76]提出了一种卷积算子ConvPoint,将卷积核划分为空间核权重和特征核权重,混合几何空间和特征空间。几何空间使用多层感知机来学习卷积核与点云之间的关系函数,即稠密加权函数,然后与特征空间加权融合得到卷积输出。这2个卷积算子在选择近邻点时均使用了二叉树(kdtree)[77]代替K近邻,并使用索引列表存储近邻点集,使得卷积对输入点云密度具有鲁棒性。
2.2.2 参数化核函数
首先,Wang等人[78]提出了一种参数化连续卷积(parametric continuous convolution)算子,依据万能近似定理(universal approximation theorem),采用多层感知机计算卷积核函数,因为它能够逼近任何连续函数,这样卷积的输出可以是整个连续向量空间中的任意点。通过级联多个该卷积算子的卷积层构建深度参数化连续卷积网络(PCCN)。然而该方法只能近似深度方向的卷积,而不能近似实际卷积。
Xu等人[79]提出了卷积算子SpiderConv,将连续卷积核函数定义为阶跃函数和定义在K近邻上的泰勒展开多项式的乘积。阶跃函数通过计算中心点及其近邻点之间的测地线距离(geodesic distance)来获取粗糙的几何结构;泰勒展开式通过在中心点及其近邻点构成的立方体顶点处进行插值来学习局部的细粒度几何结构。同样通过级联多个带有SpiderConvs的卷积层构建卷积网络SpiderCNN,与该卷积算子和网络的思想最为接近的是处理体素输入的稀疏卷积网络SparseCNN[25]。
Hermosilla等人[80]提出了一种蒙特卡洛卷积(Monte Carlo convolution)算子,Wu等人[81]提出了一种称为PointConv的卷积算子,二者均将卷积运算视为蒙特卡洛估计(Monte Carlo estimate)的过程,由权重函数和密度函数组成的非线性函数。使用多层感知机近似卷积核权重函数,采用核密度估计(kernel density estimation)学习概率密度函数(probability density function, PDF),用来重新加权学习的权重函数,这就使得蒙特卡洛可以处理不同采样密度的点云。然后分别构建了各自的蒙特卡洛卷积网络进行分层点云特征学习。
Wang等人[82]提出了一种片元卷积(PatchConv)算子,首先遍历全局空间,为每个中心点构建PointPatch模块,即以中心点为原点将3D局部邻域划分为8个卦限(octant),并搜索每个卦限中的近邻点作为该卦限的特征;如果在一个卦限内没有近邻点,就选择中心点特征作为该卦限的特征。卷积核权重函数被视为一个由多层感知机近似的利普希茨连续函数(Lipschitz continuous function),在每个挂限进行卷积运算提取中心点的高维特征。
进一步构建了一个带有PatchConvs的轻量级卷积网络PatchCNN以有效集成每个PointPatch模块中的特征。Liu等人[83]提出了一种基于邻域集合关系推断的卷积(relation-shape convolution, RS-Conv)算子作为卷积网络RS-CNN的核心,计算每个局部邻域中的近邻点与中心点之间的关系,包括低维关系(low-level),即两点坐标之间的欧氏距离和两点特征之间的相对距离;高维关系(high-level),即更抽象的点关系表示。使用多个共享多层感知机近似卷积核来学习局部邻域中点之间关系的映射。
随后,Liu等人[84]又提出了一种卷积算子PConv,将卷积运算分解为2个核心步骤:1)特征变换(feature transformation)。卷积核函数被定义为带有非线性激活器的共享单层感知机(single-layer perceptron, SLP)以提高其效率。2)特征聚合(feature aggregation)。使用聚合函数来聚合这些变换后的特征。然后基于PConv构建了DensePoint模块,所有前面层的输出都用作其输入,其自身的输出用作所有后续层的输入,这样每层都可以获得特定级别的信息。最终,聚合得到丰富的局部语义信息和全局形状信息。
由于点云的稀疏性,Atzmon等人[85]提出了一种稀疏卷积(sparse extrinsic convolution)算子并构建了相应的点卷积神经网络(PCNN)来处理点云任务,应用径向基函数(radial basis function, RBF)进行卷积,这一参数化过程没有任何的离散化操作或者近似操作。随后,Poulenard等人[86]基于PCNN[85]提出了球谐卷积神经网络(SPHNet),使用球谐(spherical harmonics)函数定义了一种非线性旋转不变卷积(spherical harmonics convolution, SPHConv)算子来实现旋转不变性。对比二者的网络结构与性能如表1所示。
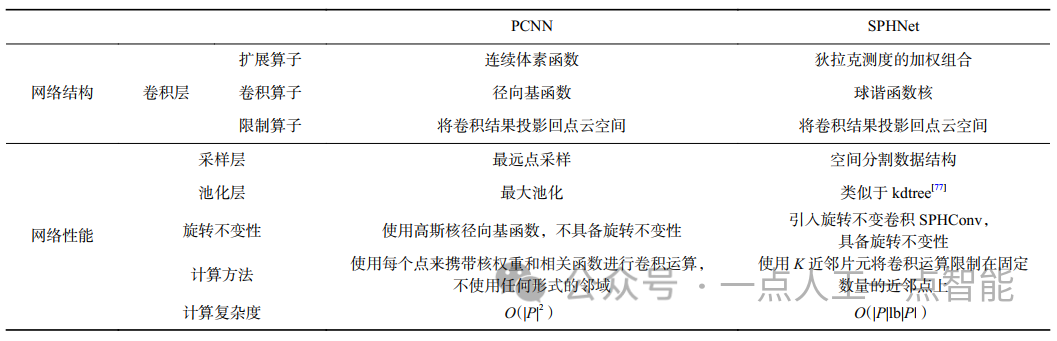
SPHNet[86]是首次强调旋转不变性对于点云分析任务重要性的研究工作,这就要求当给定任意的旋转角度或方向时,输出相同的分析结果,如之前提到的SO(3)和SE(3)[66],使网络对点云的旋转具有鲁棒性。
一种常见的解决方案是使用任意旋转来增加训练数据,但这样做的局限性是存在一些不可预见的旋转,而且由于训练数据量的增加,训练时间复杂度也会随之增大。因此为了解决这一问题,一些研究人员陆续展开了相关研究并提出了一些具有旋转不变性的点云卷积算子。
Zhang等人[87]基于两点之间的欧氏距离和角度特征,提出了一种旋转不变卷积(rotation invariant convolution, RIConv)算子。由于这些几何特征在刚性变换下是不变的,而且不像点坐标是唯一的,许多点共享相同的距离和角度,因此它们非常适合于构造具有旋转和平移不变性的卷积算子。然后使用共享多层感知机将这些几何特征从3D空间提升到高维空间,并进行卷积运算提取特征。这2种方法的优点是允许在训练/测试场景中旋转或不旋转的情况下进行一致的预测,并且鲁棒性强,可以推广到具有不可见旋转的输入数据中。
尽管如此,这2种方法的性能有时可能不如一些具有平移不变性的点云卷积算子[56,60],详见第3节。此外,由于RIConv[87]将3D坐标转换为一些旋转不变的特征,例如距离和角度,导致3D坐标编码的全局信息丢失。为了解决这一问题,GCAConv[72]利用了局部参考系(LRF),其原理是,卷积与任何映射函数一样,可以通过对齐输入与旋转等变映射(rotation-equivariant mapping)的结果,将其转换为旋转不变映射(rotation-invariant mapping),这样就将输入点云的全局特征信息集成到了卷积运算中。参考这一方法,同时由于KPConv[70]性能优异、定义直观、灵活性强,且能够直接将特征与空间定义的卷积核相结合,Thomas[88]结合旋转等变性和旋转不变性之间的内在联系[66]设计了一种旋转不变性的多对齐卷积(multi-alignment KPConv, MA-KPConv)算子。
为了能够提取更准确的信息,首先设计了一个对齐模块(alignment module),假设每个输入点都有一个旋转等变LRF,这些LRFs可以重新排列成旋转不变的LRFs,并用共享多层感知机对该信息进行编码转换为旋转不变特征,输出与输入特征尺寸相同的特征,可以视为近邻点的LRF和中心点的LRF之间的变化关系,该特征提供了有关邻域的几何信息。将输入特征与对齐特征进行连接作为标准KPConv[70]的输入进行卷积操作输出最终特征。这种变换的原理是只要LRF是旋转等变的,对应的特征是旋转不变的,这个对齐卷积的输出就是旋转不变的。
然后,设计了一个多对齐模块(multi-alignment module),假设每个输入点都有多个旋转等变LRFs,通过在每个LRF上使用对齐卷积运算以获得一组对齐输入,采用核相关性为每个对齐输入聚合核点上的特征,连接起来使用卷积核,有效地聚合来自不同对齐的信息,而不同于KPConv[70]为每个对齐输入使用单独的卷积核。但由于使用了不变性特征而减少了卷积必须学习的形状多样性,这可能会降低网络的学习能力和鲁棒性。
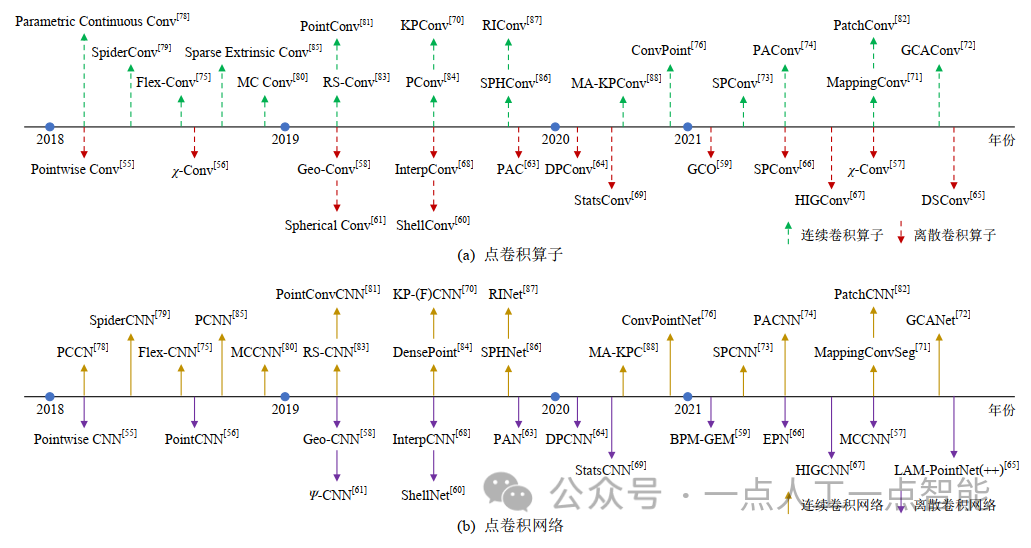
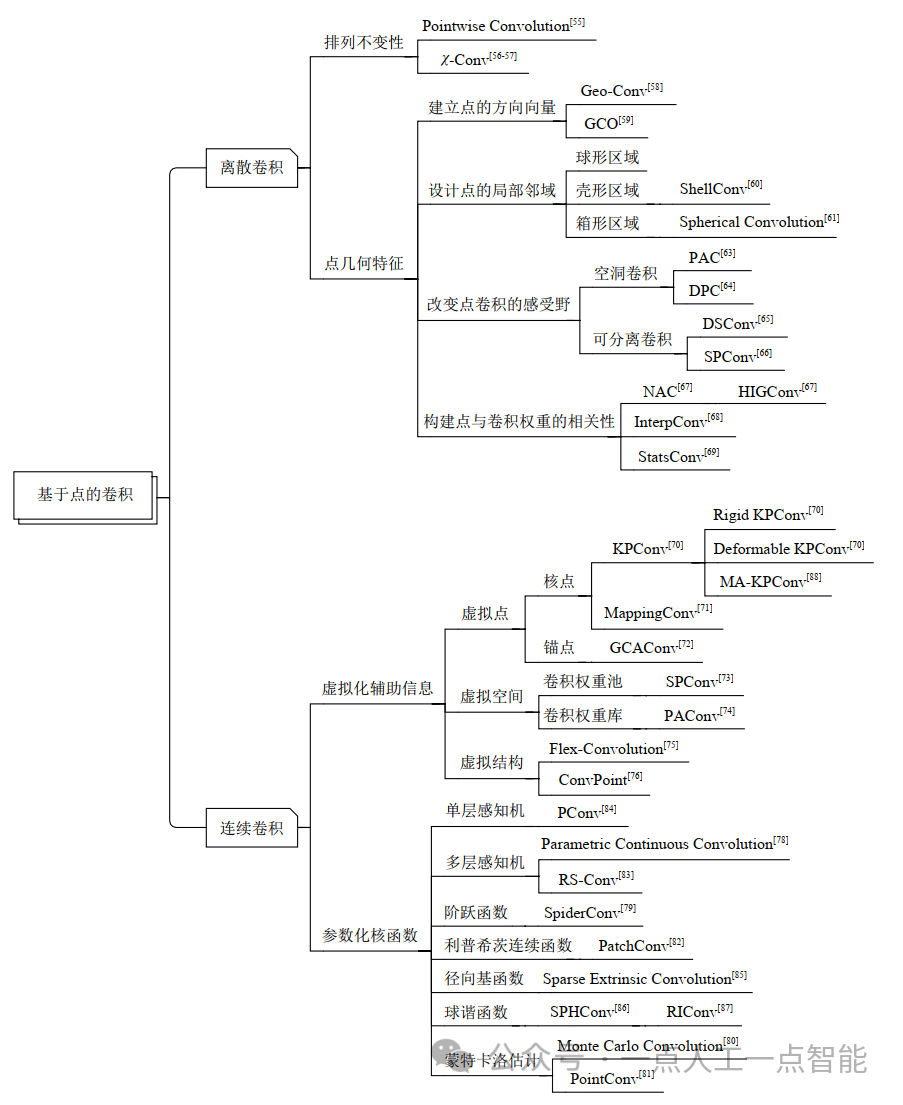
综上所述,类似于文献[3]中对点云任务的各个深度学习方法进行的较为直观的列举方法,本文按照时间顺序将现有的基于点的卷积算子(如图10(a)所示)及其对应的网络结构(如图10(b)所示)进行了整理与汇总。同时,本文为这些基于点的卷积算子搭建了一套独特的分类体系,如图11所示。此外,我们还将其所对应的卷积网络进行了分类整理,如表2所示,并对各个方法的优缺点进行了总结。与离散卷积方法相比,连续卷积方法更适合捕捉3D点云的局部几何特征。
综合分析对比连续卷积的2个策略,可以得出,有时候使用参数化表示会使卷积算子更加复杂,待训练参数较多,学习效率低下,网络的收敛性也更加困难,还容易出现过拟合,适应性较差。而使用几何特征可以保留物体最初的形状信息,但一些引入虚拟点或空间会消耗内存,其位置选取对网络的最终性能有着至关重要的影响,根据一些先验信息或规则预定义虚拟信息也一定程度上限制了网络的灵活性,导致性能会有所降低,可能需要针对不同的数据集或主干架构进行专门优化。

卷积网络应用在点云处理任务上的性能会在第3节中重点进行分析对比。
本文根据卷积运算的类型(即离散卷积和连续卷积)对各个点卷积算子及其对应的网络结构进行了分类与整理。同时,本文将围绕这些卷积方法进一步分析卷积算子的原理,对比分析基于点云的卷积网络在分类与分割等具体任务中的性能,最后进行总结及对未来相关研究的展望。
本文跟踪了点云领域最新的研究进展,并在前人工作的基础上进行了补充完善和深入挖掘。
首先,在算法内容上,本文将重点聚焦在基于3D点云的卷积运算方法上,并且添加了最近提出的基于点云的卷积新方法,总结了30多种应用于点云上的卷积运算和卷积网络,并对其进行了更深入地调研和更详细地展开,同时深入挖掘了各个卷积运算和卷积网络之间的区别与联系。
根据3D点云数据处理方式,将它们分为2类:离散卷积和连续卷积。关于离散卷积,细分为针对点的排列不变性进行的卷积运算和针对点的几何特性进行的卷积运算;关于连续卷积,细分为添加虚拟化辅助信息后进行卷积运算和参数化核函数后进行卷积运算。
与以上综述[47-53]相比,本文从学习方法的角度而非点云任务的角度来探讨现有文献如何对在点云上的卷积运算和卷积网络进行设计,从而进行更充分的特征提取,使得其更好地服务于下游的特定任务,包括点云分类和分割。其次,在应用内容上,本文归纳了基于点的卷积神经网络的基本框架,并在此基础上整理了现有研究中分类和分割网络的具体网络结构,此外还增加了对常见的真实场景数据集的介绍与对比工作。最后,在未来研究方向上,本文在基于3D点云的卷积运算技术评述的基础上,对点云领域未来研究方向进行了展望并给出各类技术的参考性价值。
03 点云任务应用
针对第2节提出的关键要求3),本文综述的各类研究工作的思路一般包括3步:
首先将其提出的点云卷积算子集成到分类或分割网络框架中;然后将各个集成后的网络应用到点云分类、分割等任务中进行实验分析;最后根据实验结果通过对比集成后的网络与原始网络的性能来进一步验证所提出的点云卷积算子的有效性和优越性。
鉴于点云分类、分割任务是3D目标检测与跟踪、3D场景重建与理解等更复杂且重要的下游任务的基础,在本节中,我们选取4个常见点云任务来进一步分析研究,如表3所示,通过对比各个点云任务的结果来分析由不同点云卷积算子集成后的网络的性能,从原理上挖掘卷积方法取得相对较优结果的原因,深入探索各个卷积运算的优劣,从而给出一些对未来更深入研究的建议与启发。

3.1 网络框架
大多数研究工作中涉及到的分类与分割网络的基础框架与2D图像的卷积神经网络框架相似,如图12所示,其中,类似于LeNet-5[6]的分类网络,首先经过包含1个或多个串联的卷积层的编码器对点云进行特征提取和变换,采用不同的卷积算子以逐层提取输入点的特征,点的数量逐渐减少,点特征的维度逐渐增多;然后再经过包含1个或多个全连接层的分类器(classifier)对点云进行归类,最终得到分类结果。
类似于U-Net[9]的分割网络,是一个具有跨层连接(skip connections)的编码器-解码器(encoder-decoder)体系结构。分割网络与分类网络共享同一个编码器,主要用于特征提取(feature extraction),经过编码器中的卷积层提取到的特征称作局部特征,包括了每个点特征和点之间的关系特征。
解码器主要用于特征传播(feature propagation),由于分割任务是逐点的标签预测,所以需要将特征输入到解码器中,经过反卷积层或者其他操作(如插值、池化)进行特征扩展使得点云达到原始分辨率,点的数量逐渐增多,点特征的维度逐渐减少,得到的特征称作全局特征。最终将局部特征和全局特征逐层连接起来,就可以得到用于分割任务的全部信息,同一个集合的点具有相似或相同的属性和标签,因此要归为同类(即物体上的某一个部件或场景中的某一类物体)。
需要注意的是图12的网络框架图只包含了网络的最主要部分,即卷积层(该层是各个网络的核心,与所使用的卷积算子有关,内部结构均不相同)、反卷积层、全连接层,其余的如池化层、上采样层、插值层、批归一化层、激活函数层等,在具体网络具体涉及到的层数和连接顺序均有所不同,具体网络结构如表4所示。


第2节中总结的基于点云的卷积算子大多是即插即用的,在不改变其他原始的网络配置(如网络层数、特征通道数)的情况下,将某个卷积算子(***Conv)嵌入到经典的点云任务网络中,以评估该算子的有效性并最大程度地减少复杂网络架构的影响。
关于这些网络,它们统一的训练流程大致如图13所示,其中,最重要的部分就是集成了特定卷积算子的卷积层作为特征提取模块,特征提取不充分将严重影响点云分类和分割任务的精度。
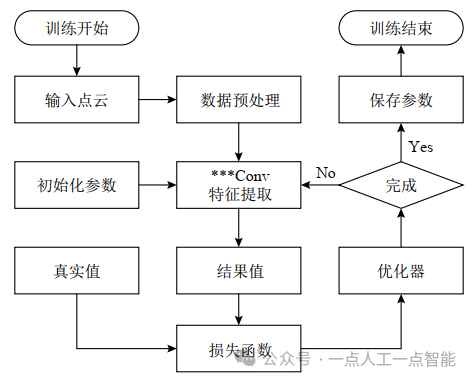
接下来,本文重点对比分析了形状分类、部件分割、语义分割、法线估计这4个具体任务中各个网络的性能。
需要注意的是,由于部分论文代码未开源,无法在同一个实验设备、相同网络参数的情况下一一复现本文综述的所有卷积方法,我们借鉴了近些年来的大多数综述论文(如文献[3])的结果处理方式,提取各个论文中给出的对比结果并进行了归纳总结。因此,这里的实验结果仅考虑了在相同评价指标和相同数据集的前提下进行对比分析。
由于各个研究工作所使用的软硬件条件和实验环境可能各不相同,卷积算子所集成的基础网络框架也各不相同,最终的性能对比结果的准确性也会有所影响,最终得到的结果也属于相对较优值而非绝对最优,其他具体情况还需进一步具体分析。
3.2 形状分类
参考关于深度学习在点云上的研究综述[3],本文整理了相关的用于3D点云形状分类任务的数据集和评估指标,并在此基础上,对各个卷积网络的性能进行了对比分析。
1)数据集。为了测试不同的卷积运算在3D点云形状分类任务中的结果,现有研究工作使用的公开数据集主要是合成数据集(synthetic datasets)——ModelNet10/40(2015)[89]。ModelNet数据集包含了来自662个类的127915个3D目标物体,其子集ModelNet10包含了来自10个类的4899个目标物体,ModelNet40包含了来自40个类的12311个目标物体。数据集中的目标物体是完整的,没有任何遮挡和背景噪声的影响。注意:由于在ModelNet10数据集上进行分类实验的研究工作数量较少,这里忽略不计,仅对比在ModelNet40数据集上的结果。
2)评价指标。为了评估这些卷积运算在3D点云形状分类任务中的性能,现有论文提出了不同的分类网络性能评价指标,常用指标为:
①总精度(overall accuracy, OA)。被正确分类的类别数与总类别数之间的比值。该值虽然能很好地表征总体分类精度,但对类别个数较多且不平衡的数据集来说影响较大。
②平均类精度(mean class accuracy, mAcc)。每个形状类别内的被正确分类的个数与总个数之间的比值。该值适用于类别个数较多且不平衡的数据集,可以表征各自类别的分类精度。
3)对比结果。表5列举了各个研究工作中的点云分类网络在形状分类任务上的性能并进行了结果对比,主要包括输入类型(点坐标P/法向量N)和2个评价指标在ModelNet40数据集上的结果。为了更全面地对比各个卷积网络的性能,表5中除了列举了基于点的卷积网络外,还列举了引言中提到的一些其他的有代表性的方法,包括先驱工作PointNet[4]和PointNet++[5]、基于投影的方法ACNN[14]和A-CNN[16]、基于体素的方法3DmFV-Net[23]、基于晶格的方法SFCNN[26]、基于图的方法SPH3D-GCN[43]。
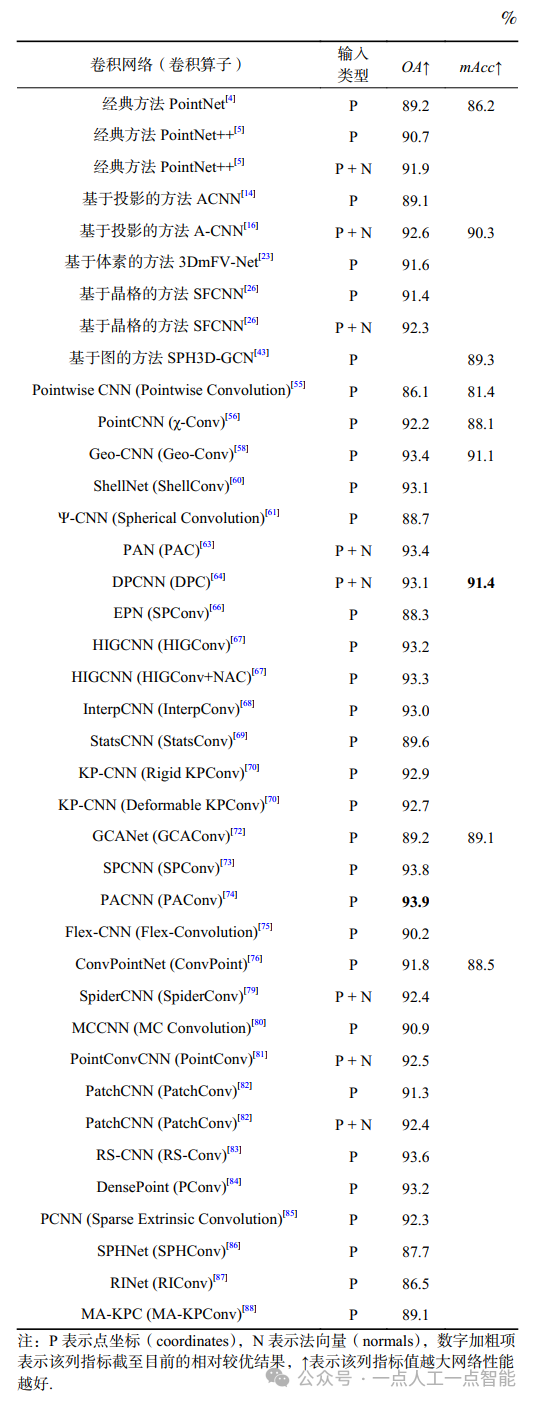
4)结果分析。OA值是针对整个数据集的全体数据来说的(不区分类别),而mAcc值则是先计算每一个类别的准确率,再取平均值。当每个类别的数据量相等时,则OA值等同于mAcc值;反之,OA值主要受数据量相对较大的类别的准确率影响,mAcc值则主要受数据量相对较小的类别的准确率影响。也可以认为OA值和mAcc值的差别在于对每种类别的准确率其权重不同,OA值是根据该类别数据量与总数据量比值率确定权重,而mAcc值是平均分配。
通过分析这2个评价指标的区别,我们可以得出,并不是OA值最优的网络其mAcc值就一定也是最优的,二者的侧重点是不同的,因此,本文通过单独对比各个网络的OA值和mAcc值并找到各自指标下相对较优值,对其进行原理上对某些方法取得较优结果的原因进行深入探索。
对比各个网络的OA值可以得出目前相对较优的网络是PACNN[74],这是由于卷积算子的灵活性和网络架构的简洁性,首先构造了一个可学习的卷积权重库,其次将即插即用的卷积算子PAConv直接集成到一些经典点云网络架构,包括PointNet[4]、PointNet++[5]、DGCNN[39]中,分别替换原先编码器中的MLP和EdgeConv,而不更改原有的网络配置,最大程度地减少了复杂网络架构的影响,使得PAConv的有效性大大提升。
同样,OA值仅次于PACNN的SPCNN[73]也定义了一个可学习的卷积权重池,网络也类似于PointNet++[5]。且二者均采用自适应学习的方式,即选择合适的基本权重矩阵和通过3D空间中点的位置关系学习得到的相关系数向量来构造卷积核,以更好地处理不规则和无序的点云数据。
不同之处在于,PAConv采用了一个分数网络来学习,而SPConv通过构造几何引导的索引映射函数来实现。相比于PACNN、SPCNN的结果较差的原因可能还因为其网络层次相对较深,构造了一个具有多层次结构的卷积网络,因此复杂网络架构虽然降低了其性能但影响不大。在今后的研究中可以选择将PAConv或SPConv集成到其他任务网络中以帮助提升结果的准确性和高效性。
类似地,对比各个网络的mAcc值可以得出目前相对较优的网络是DPCNN[64],这是由于该空洞点卷积显著增加了点卷积的感受野大小,其所涉及的空洞机制也可以很容易地集成到大多数现有的点卷积网络中。空洞卷积通过动态调整空洞率,在不丢失空间分辨率的情况下扩大卷积感受野,由此获得多尺度信息。
在未来的研究工作中,在此基础上通过引入空洞率随网络深度增加而增大的动态空洞点卷积来进一步讨论卷积网络性能也可能是一个更有研究价值的方向,这样的网络可以在初期学习局部特征,在后期学习更高级别的信息。
3.3 点云分割
根据分割粒度可以将点云的分割任务分为部件级的部件分割、对象级的实例分割、场景级的语义分割[3],3者之间的区别示例如图14所示(来源:ShapeNet数据集、S3DIS数据集、SemanticKITTI数据集)。
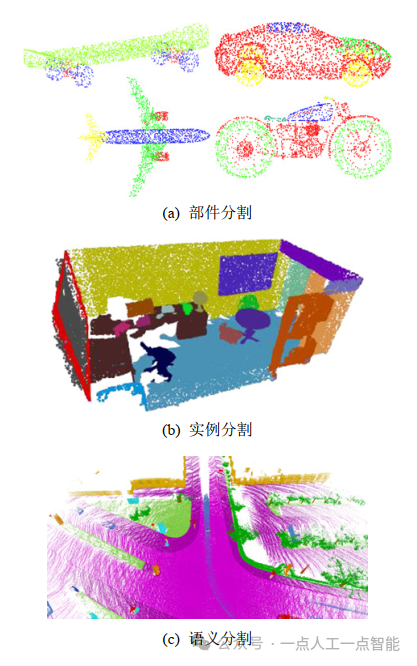
具体来说,点云语义分割是根据点的语义信息把点云划分为若干个特定的、具有独特性质的子区域并识别出点云内容打上类别标签的任务。不区分不同的目标,也就是将相同类别的不同目标归为同一个标签。
与语义分割相比,点云实例分割更具挑战性,它需要更精确和细粒度的点推理,不仅需要区分具有不同语义信息的点,而且需要区分具有相同语义信息的实例,也就是识别并区分出各个目标,归为不同的标签。部件分割则是区分某个实例的各个部位并打上不同的类别标签的任务。
但由于实例分割任务在应用较少,这里不再对场景级的点云实例分割任务作进一步的分析对比研究。同样,参考关于深度学习在点云上的研究综述[3],本文分别整理了相关的用于3D点云部件分割与语义分割任务的数据集和评估指标,并在此基础上对各个卷积网络的性能进行了对比分析。
3.3.1 部件分割
1)数据集。为了测试不同的卷积运算在3D点云部件分割任务中的结果,现有研究工作均使用了ShapeNet(2015)[90]这一合成数据集。ShapeNet数据集包含了约300万个3D目标物体,其子集ShapeNetCore包含了来自55个类的51300个目标物体。
2)评价指标。为了评估这些卷积运算在3D点云分割任务中的性能,现有研究工作提出的评价指标主要是均交并比(mean intersection over union, mIoU)。在每个类上计算交集和并集之比的平均值即为类均交并比(class mIoU);在每个实例上计算交集和并集之比的平均值即为实例均交并比(instance mIoU)。
3)对比结果。表6列举了各个研究工作中的点云分割网络在部件分割任务上的性能并进行了结果对比,包括输入类型(图像I/点坐标P/法向量N)和2个评价指标在ShapeNet数据集上的结果。为了更全面地对比各个卷积网络的性能,表6中除了列举了基于点的卷积网络外,还列举了引言中提到的一些其他的有代表性的方法,包括先驱工作PointNet[4],基于投影的方法A-CNN[16],基于体素的方法SparseConvNet[20]和PVCNN[22],基于晶格的方法SPLATNet3D[25]、SPLATNet2D-3D[25]和SFCNN[26],基于图的方法SPH3D-GCN[43]。
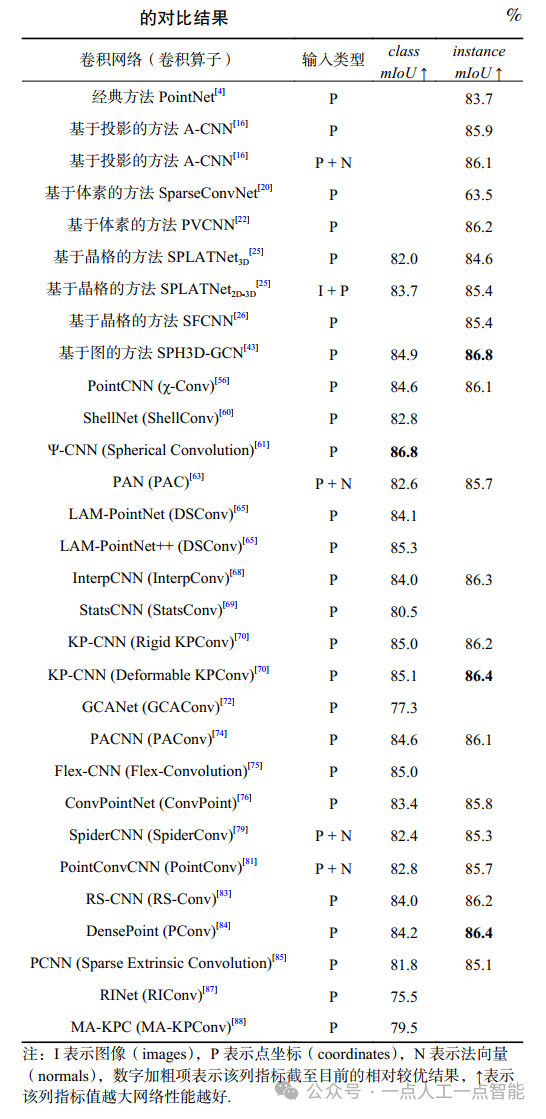
4)结果分析。部件分割任务最大的难点就是具有相同语义标签的实例具有较大的几何变化和模糊性。对比各个网络的class mIoU值,可以得出目前相对较优的网络是Ψ-CNN[61],其所使用的卷积算子Spherical Convolution是目前性能较好的。Ψ-CNN[61]着重研究分析了不同的点局部邻域搜索策略。显然,对于不同结构的点云,应该采取不同的点局部邻域搜索策略,例如球查询、K近邻、树结构(kdtree, octree)。
相比之下,球查询、K近邻是直观的、简单的,但对于点数更多的输入点云,树结构显然是更有效的,因为点的局部邻域信息更容易获得,这就提升了Ψ-CNN[61]的计算效率。如果点云是稀疏的,分布很广泛且没有规律可循,如某个真实场景,kdtree能更好地划分物体与背景,而octree则很难决定最小立方体的尺寸应该是多少,太大则一个立方体里可能有很多不同标签的点云,太小则可能立方体之间关联不起来。如果点云分布非常规整且聚集,如某个特定物体,则octree更容易求解凸包,并且点与点之间相对距离无需再次比对父节点和子节点,更加明晰。因此,Ψ-CNN[61]这一基于八叉树结构的网络,可以更高效地探索物体各个部件的几何信息和几何变化,具有相对更优的网络性能和对比结果。
类似地,对比各个网络的instance mIoU值,可以发现,基于图的方法SPH3D-GCN[43]要普遍优于其他方法,这是由于离散核、可分离球卷积和基于图的体系结构的结合增加了该方法的可扩展性和灵活性,增加了网络的性能。其中,采用不同的离散核可以识别相同邻域的不同特征;引用可分离球卷积策略分别执行深度卷积运算和点卷积运算,显著减少了网络的参数数量和计算成本;使用更灵活的基于图的体系结构设计网络架构,保证了网络在更接近标准CNN的同时还能更好地处理大规模点云数据,计算效率较高。因此,除了直接处理离散点数据的卷积网络,处理图数据的卷积网络也是研究人员倾向于深入研究的方向。
此外,KP-CNN[70]是基于点的卷积方法中相对较优的,其中,可变形KPConv的性能较刚性KPConv的性能要稍好一些,这是由于可变形KPConv具有更强大的点特征描述能力以及可学习性。
3.3.2 语义分割
1)数据集。语义分割一般用于真实场景中进行场景与物体之间的分割任务,将目标与背景之间进行分割。现有的较为常用的真实场景数据集(real-world datasets)均是由不同类型传感器获取得到的。这里列举并比较了4个在点云分割任务研究中使用较多的真实场景数据集,如表7所示。与合成数据集不同的是,这类数据集由于传感器本身固有的物理特性限制、扫描过程中的路线或位置限制(如建筑物的顶部),最终得到的点云会有不同程度的遮挡、空洞和噪声,因此训练和测试的难度较合成数据集来说要大很多,是极具挑战性的。

2)评价指标。为了评估这些卷积运算在3D点云分割任务中的性能,现有论文提出了不同的评价指标,常用的性能指标主要包括OA和class mIoU。
3)对比结果。表8列举了各个研究工作的点云分割网络在不同数据集的语义分割任务上的2个评价指标的对比结果,由于在SemanticKITTI数据集上的结果较少,故这里不展开分析。同样,为了更全面地对比各个卷积网络的性能,表8中除了列举了基于点的卷积网络外,还列举了引言中提到的一些其他的有代表性的方法,包括先驱工作PointNet[4]和PointNet++[5]、基于投影的方法A-CNN[16]、基于体素的方法PVCNN和PVCNN++[22]、基于图的方法SPH3D-GCN[43]。

4)结果分析。从表8中可以看出,HIGCNN[67]在室内数据集S3DIS和室外数据集SemanticKITTI上均取得了相对较优的class mIoU值,该网络最显著的特点是轻量级,采用较少的参数,消耗较低的计算成本和内存成本,充分挖掘点云的细粒度几何特征,自适应地进行特征选择,增强有用的结构特征和抑制无用的噪声特征,在保证获得更好性能的同时复杂度更低、准确性更高。
卷积算子ConvPoint[76]在室内数据集S3DIS和室外数据集Semantic3D上均取得了相对较优的OA值,该卷积方法是稀疏化和非结构化数据在离散卷积上的推广方法,具有灵活性和计算效率高的特点,其中,各个点和卷积核元素之间的几何关系是相对的,由此降低了对输入点云大小的敏感性,可以构建各种网络体系结构。
此外,KP-CNN[70]在室内数据集ScanNet上取得了相对较优的class mIoU值,在室外数据集Semantic3D上取得了次优的class mIoU值。从数据集上来看,这些真实场景数据集中的3D场景范围较大,因而无法作为一个整体进行分割任务。
而KP-CNN[70]采用随机选取的球体来将一个整体场景点云分割成多个子云(subclouds),确保每个点都由不同的球体预测多次,这就保证了每个点的预测概率是平均的。
通过计算每个输入点对不同位置的KPConv层输出结果影响相对于输入点特征的梯度,即有效感受野(effective receptive field, ERF),可以发现,刚性KPConv的ERF对每种类型的对象都有相对一致的度量范围,而可变形KPConv的ERF具有更强的自适应性,可以适应不同类型对象的大小,提高了网络适应场景的几何结构的能力,并能够从场景中获取更多的细节信息,其在室内数据集S3DIS上具有更好的性能。
然而在更具多样性对象更丰富的室内数据集ScanNet和室外数据集Semantic3D上,刚性KPConv的性能较可变形KPConv的性能要稍好一些,这是由于可变形KPConv在提升了点特征描述能力的同时会增加整个网络的复杂性,可能会干扰网络的收敛或导致过拟合。
3.4 法线估计
表面法线是3D点云的重要属性之一,在很多领域都有大量应用,例如,在进行光照渲染时产生符合可视习惯的效果时需要表面法线信息才能正常进行。大部分点云任务的处理也都要用到法线,包括点云平滑滤波、点云配准、点云曲率计算等。此外,估计一个点云的表面法线是3D重建任务的一部分[85],性能优劣将直接影响到后续的重建结果。
表面法线估计任务可以看作是一个有监督的回归问题,近似于估计表面某个相切面的法线,需要对每个点进行预测。因此,也可以通过改变点云分割网络的一些超参数来适应这项任务。
本文将涉及法线估计的研究工作进行了对比分析,结果如表9所示,采用的数据集是ModelNet40[89],对比的性能指标是余弦损失(cosine loss)。同样,为了更全面地对比各个卷积网络的性能,表9中除了列举了基于点的卷积网络外,还列举了引言中提到的一些其他的有代表性的方法,包括先驱工作PointNet[4]和PointNet++[5]。
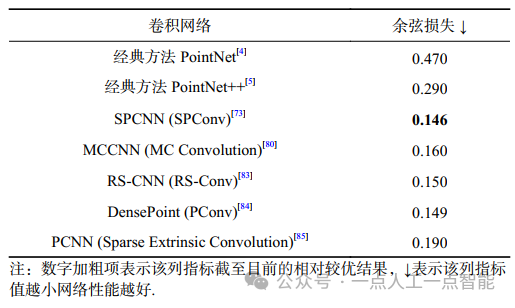
由表9可以得出,对于法线估计任务,相对性能较优的卷积网络和算子是SPCNN(SPConv)[73],该卷积方法通过几何引导权重选择来推广图像卷积,自适应地划分点云中的几何学习空间。图像像素排列规则,因此权重和像素具有确定的索引对应关系。然而,对于不规则地分布在连续3D空间中的3D点云,这些索引对应关系是未知的。因此,该研究工作构造了一个几何引导的索引映射函数,该函数隐式地在卷积权重和邻域中的一些局部区域之间建立对应关系,学习自适应地划分并感知点云的局部几何结构,高效地用于点云分析任务中。
最后,综合分析形状分类、部件分割和语义分割这3类有代表性的点云任务。在这3类云任务中均进行了实验和分析的研究工作,主要包括:PointCNN (χ-Conv)[56],ShellNet (ShellConv)[60],PAN (PAC)[63],InterpCNN (InterpConv)[68],KP-CNN (Rigid KPConv)[70],KP-CNN (Deformable KPConv)[70], PACNN (PAConv)[74],ConvPointNet (ConvPoint)[76],PointConvCNN (PointConv)[81],MA-KPC (MA-KPConv)[88],对比结果如图15所示。
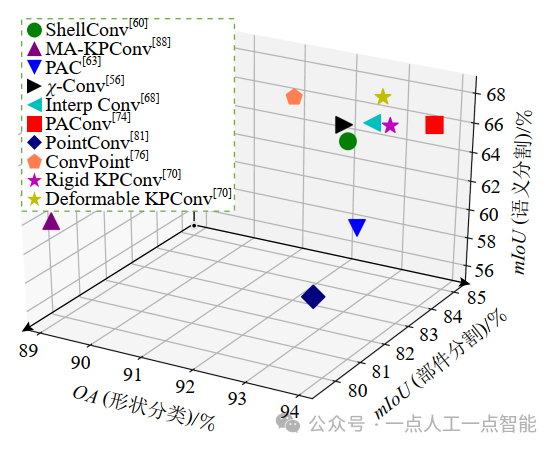
结合表5、表6、表8的对比结果可以得出,相对较优的结果均为连续卷积中构造虚拟化辅助信息的卷积算子,包括在点云分类任务中的PAConv[74]、在点云分割任务中的KPConv[70]、在点云法线估计任务中的SPConv[73]。
相比较而言,KPConv[70]这一即插即用卷积算子在今后的研究中可作为集成到各种点云任务网络中的首选,如MA-KPC[88],虽然对比结果显示该网络在KPConv[70]上进行的改进性能并没有提升,但其研究重点在于解决点云的旋转不变性问题,且实验表明通过任意角度的旋转所得到的结果均是最优的,同时,MA-KPC是首个在S3DIS这一大型室内场景数据集的分割任务中进行旋转不变性问题的研究并得到了较优的结果的网络,虽然,许多真实场景由于重力定向(gravity-oriented)原因只能绕z轴自由旋转,整个场景的任意角度旋转可能没有实际应用价值,但场景中的某些小型目标可以进行任意旋转,例如掉落在地上的物体,虽然不常见,但在实际应用中可能会影响分析结果。今后的研究还可以针对MA-KPC所面临的其他困难与挑战继续深入。
04 总结与展望
卷积运算的核心在于对特征的局部聚合和学习,经过近些年的不断发展,通过大量的实验分析与对比,各种各样卷积运算和卷积网络的提出在理论上和实践上都被证实其是处理不规则数据格式的一种有效方法和框架。
本文全面概括和提炼了近年来研究工作中提出的各种各样新颖的可直接作用于点云上的卷积算子,分类并分析了这些卷积算子的结构和卷积运算的原理。同时,针对研究工作中所涉及到的集成了这些卷积算子的基础任务网络,包括点云分类网络和点云分割网络,从设计的网络结构、采用的公开数据集、使用的评价指标等方面进行了分类整理与性能对比,总结了相对较优的卷积算子和卷积网络,以助力一些下游的点云任务,如3D目标检测与跟踪、3D场景与目标分割等。虽然,卷积运算具有一定的优势,但目前仍然存在一定的不足和待完善之处。
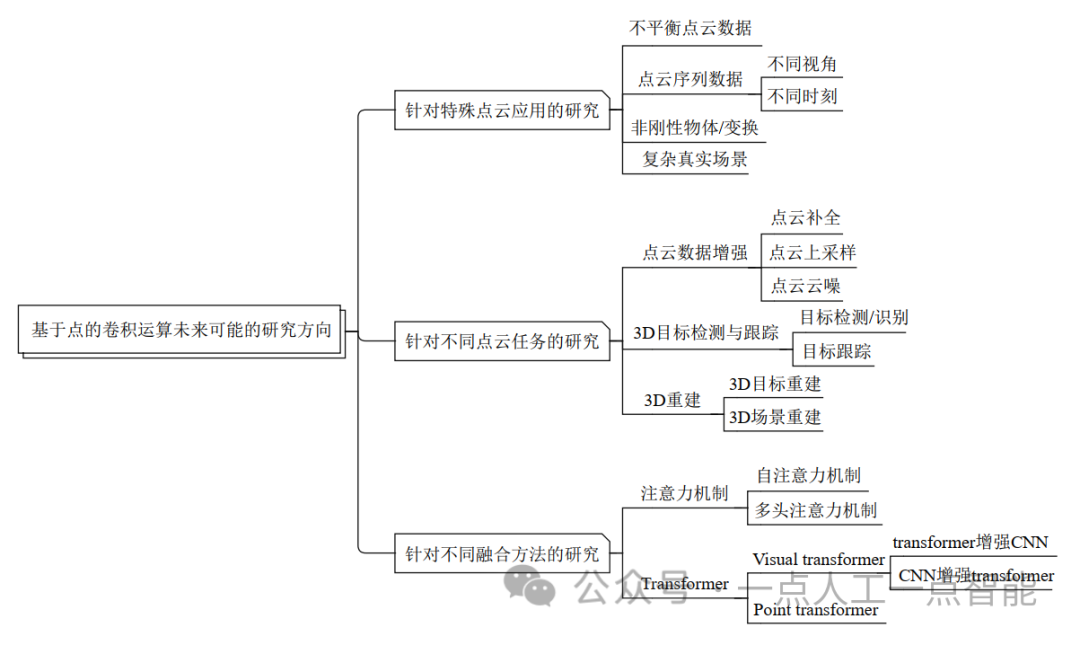
此外,本文探讨并列举了3个关于基于点的卷积运算的一些未来可能的研究方向,主要包括针对特殊点云应用的研究、针对不同点云任务的研究、针对不同融合方法的研究,如图16所示。
4.1 针对特殊点云应用的研究
1)不平衡点云数据
从第3节不同任务的OA值和mAcc/mIoU值的比较结果可以发现,尽管一些方法[70,76]都取得了显著的总体效果,但它们在类别相对较少的情况下表现仍然有限。基于类别不平衡的点云数据的特征学习仍然是点云任务(尤其是分割任务)中一个具有挑战性的问题。
2)点云序列数据
一些实际应用场景中有时需要对3D传感器在不同视角或不同时刻下捕获的点云序列数据进行处理,如动作捕捉、3D重建。
①不同视角的点云序列。利用不同视角点云之间的点匹配估计运动物体在3D空间中的变换关系,包括旋转、位移。②不同时刻的点云序列。利用不同时刻点云之间的特征匹配估计运动物体在3D空间中的运动信息,包括速度、角速度、动量等。
这2个匹配估计流程通常包含2个基本步骤:局部特征描述和全局特征匹配。
因此需要网络具有一定的鉴别能力来区分相同目标物体内部或不同目标物体之间的局部几何结构。这就对特征提取和特征匹配提出了更高的要求。然而,现有的提取点云局部和全局特征的方法仍难以充分满足这类需求,而且对于原始数据和应用场景的变化较为敏感。因此,这也是今后的一个重要的研究方向,且具有重要的实际应用价值。
3)非刚性物体/变换
刚性物体(rigid body)发生的刚性变换是平移和旋转,而相比于刚性物体,非刚性物体(non-rigid body)就是会发生形变(即伸缩、仿射、透射等比较复杂的非刚性变换)的物体。对于非刚性3D模型,点的坐标特征受姿态变化(pose variation)和非刚性变换(non-rigid deformation)的影响,因此局部的变化对网络的性能要求较高。目前在图像中的非刚性物体研究比较广泛[95],因此结合基于点的卷积算子进行非刚性点云物体的局部特征提取和相关任务研究也是一个较为新颖的方向。
4)复杂真实场景
在许多实际应用中,传感器获取的点云通常是大规模的且较为复杂的,例如目前自动驾驶领域研究使用最广泛的KITTI数据集[96]。但大多数现有方法都适用于小型点云数据(点数较少),在大型点云数据上的效果较差。因此有必要进一步研究适合在大规模点云任务上应用的卷积算子和卷积网络,进一步在降低计算复杂度的同时提升算法性能。
4.2 针对不同点云任务的研究
本质上,卷积网络中的卷积运算就是特征提取的过程,由于点云数据的特殊性,而产生了各种各样的可作用于点云上的卷积算子进行卷积运算,由于其即插即用的特性,这样的卷积算子除了用于点云分类、分割网络以外,还可以用于其他的需要进行特征提取的网络。
1)点云数据增强
实际上,许多3D扫描设备直接获取的点云数据质量会受到很多因素的影响,例如物体之间的遮挡、扫描精度降低、扫描过程中的路线或位置限制等,可能产生质量较差的点云,存在空洞、稀疏、离群点和噪声点等。因此,点云补全(point cloud completion)[97]、点云上采样(point cloud upsampling)[98]、点云去噪(point cloud denoising)[99]等点云数据增强任务也是研究的一个热点,将这些基于点的卷积算子集成到这些特定点云任务的网络中用于特征提取也是一个研究方向。例如,可以将具有旋转不变性的卷积算子集成到点云补全任务的网络中,通过多个维度的旋转及特征提取,对点云进行多个角度的补全,从中选择最优的补全结果。
2)3D目标检测与跟踪
点云分类、分割任务是3D目标检测/识别、3D目标跟踪等更复杂且重要的下游任务的基础。
典型的技术路线一般包括:目标分类/分割(对前景与背景进行分类,将背景剔除)→目标检测/识别(定位目标,确定目标位置及大小;定性目标,确定目标类别)→目标跟踪(追踪目标的运动轨迹)。
在这一过程中,特征提取占据很重要的部分,将这些卷积算子集成到这些特定任务的网络中用于高维特征提取也是一个研究方向。
相关领域的应用有:在机器人领域的动作捕捉及位姿估计;在自动驾驶领域的障碍物识别与避碰;在国防领域的精准目标打击。
3)3D重建
点云的特征提取是3D目标重建、3D场景重建等更复杂且重要的点云任务的一部分。一个具体的3D重建过程主要包括点云数据预处理、分割、三角网格化、网格渲染。实现高精度、高效率的点云3D重建也是今后重要的研究方向之一。相关领域的应用有:在遥感领域的特殊场景(如地形)的拼接及重建;在文化遗产保护领域的古文物数字模型库(如故宫数字博物馆)的恢复与构建。
4.3 针对与不同方法融合的研究
除了卷积运算外,还有很多方法已成功用于3D点云数据处理中,例如,注意力机制、Transformer。将它们各自的优势与基于点的卷积算子进行结合也是今后研究的一个趋势。
1)注意力机制
卷积运算在捕获局部特征方面有很强的优势,但在全局范围建模方面效率很低。相比之下,注意力机制可以有效地模拟特征之间的全局范围关系,但存在过度平滑问题[100]。因此,将二者结合得到的注意力卷积[62-64]可以更好地在全局信息聚合(注意力)和局部信息建模(卷积)之间建立某种联系。同时,采用不同的变体机制,如自注意力机制(self-attention mechanism)、交叉注意力机制(cross-attention mechanism)、多头注意力机制(multi-head-attention mechanism)等,与基于点的卷积运算的结合也是今后可以研究的一个方向。
2)transformer
transformer是一种基于注意力的编码器-解码器架构,最近在机器视觉领域引起了人们极大的研究兴趣。与传统的深度学习网络相比,transformer架构层次容易加深且具有更小的模型偏差,通常以自监督方式在大量训练数据上对模型进行预训练,有助于模型学习通用表征,进而针对下游任务在较小的数据集上进行微调。
受到自然语言处理(NLP)领域中基于transformer的预训练方法[101]可以显著提升性能的启发,计算机视觉领域的研究人员也提出了视觉transformer(ViT)[102]用于各类视觉任务(如分类、分割)中。
一项研究表明transformer在理论上具有比CNN更强大的建模能力[103]。然而,它的计算成本也随着特征分辨率呈二次方增长。一些研究工作尝试通过transformer和CNN的组合方法解决这一问题(如BoTNet[104],DeiT[105],ConViT[106],CeiT[107]等)。①transformer增强CNN:将transformer插入CNN主干或替换部分卷积运算。②CNN增强transformer:利用适当的卷积偏差来增强transformer并加速其收敛。
同时,transformer模型特别适合于处理不规则的点云数据,因为transformer的核心即自注意力算子本质上是一个集合算子,它对输入元素的排列和基数是不变的,而点云本质上是不规则地嵌入在3D空间中的集合。因此,有研究工作为各种点云任务构建了Point transformer网络[108],将自注意力算子应用在每个点周围的局部邻域以及点云网络中位置信息的编码。类似地,如何更高效、更鲁棒地将transformer和基于点的卷积运算相结合并应用到点云任务中也是未来的一个研究热点。
总之,随着越来越多对3D扫描设备的普及和对3D点云数据的关注,现有的卷积算子和网络可以解决一些点云处理相关的问题并得到较优的结果,但还有进一步提高和改进的空间。在未来的研究道路上,还可能有更多原理简单、训练高效、性能优异的卷积算子和卷积网络相继被提出,这会是在3D视觉领域中未来很长一段时间内的研究热点。