作者:韩超,陈敏,黄宇昊,赵明辉,杜乾坤,梁庆华
来源:上海交通大学学报
编辑:东岸因为@一点人工一点智能
同步定位和建图(SLAM)是实现机器人在未知环境下的定位和移动的重要技术方法[1]。定位精度是井下巡检的核心指标,高精度的定位算法是巡检过程中导航和避障的基础。但井下环境复杂,具有低照度、弱纹理、图像特征难以识别的特点[2],给基于视觉的SLAM算法带来了极大的困难。而激光SLAM算法测量距离远、精度高,利用环境的结构特征进行定位[3],在井下环境中更具应用前景[4-5]。
目前,SLAM算法通过估计的相邻帧之间的位姿变换不断叠加进行位姿信息计算,随着巡检时间的增加,每次位姿估计中的偏差不断累积形成较大的累积误差,制约了算法的定位精度。
利用图像语义信息丰富的特点,视觉SLAM算法如ORB-SLAM[6]、VINS[7]等,多使用基于词袋模型[8]的回环检测方法,利用预先训练的视觉特征单词构建词典,将图像中的特征描述为一个单词,图像中单词种类和数量构成图像的词袋向量,通过词袋向量之间的相似度进行回环检测。
但激光雷达分辨率低,传递信息不如图像丰富,基于词袋模型的回环检测方法难以应用。在LeGO-LOAM[9]和LIO-SAM[10]等激光SLAM方案中使用基于里程计的回环检测方法,通过当前位置信息判断是否可能存在回环,如当前位置一定范围内,存在历史轨迹点,则与对应关键帧进行匹配,并通过迭代最近点(ICP)配准方法进行位姿计算,实现累计误差的校正。此类方法效果受巡检距离限制,当累积误差超过一定范围时出现无法检测到回环或错误检测的问题,仍未解决累积误差不断增长的问题,受传感器精度影响大,且ICP方法对全部点云进行配准计算,计算时间较长。
文献[11-12]通过正态分布变换(NDT)或特征直方图检测闭环,通过距离信息判定当前位置阈值与历史轨迹的一致性,使用NDT方法或特征直方图方法进行位姿估计与二次回环检测,有效提升了匹配准确率,但召回率以及回环检测的实时性无法适用于井下无人机的定位需求。因此,使用回环检测方法解决井下无人机巡检保持长时间高精度定位的问题,需避免对里程计的依赖,使用场景相似特征进行回环检测,同时提高计算效率,保证实时性。
本文提出一种适用于激光SLAM的点云全局特征描述子回环检测方案,不依赖于位姿信息,利用矿井通道的几何结构特征进行匹配,通过计算与误差较小的历史场景之间的位姿变换,消除累积误差,并完成了完整SLAM算法框架的搭建,实时性好。该框架里程计部分基于激光里程计和建图(LOAM)[13]算法计算不带回环的位姿信息,回环检测部分基于曲率划分的特征点与点云质心之间的角度关系和尺度关系进行相似度检测,使用平面点和边角点配准方法优化计算速度,并由因子图优化方法保证全局一致性。最终,通过仿真和开源数据集实验验证了所提算法的有效性,本文研究可为激光SLAM的全局特征提取及回环算法提供理论基础。
01 基于全局特征描述子的回环检测
设计的定位系统整体分为2个模块:里程计模块和回环检测模块。
里程计模块参考LOAM算法[13]实现,输出里程计位姿信息,并根据点云三维曲率完成了特征点云的筛选,将边角特征点云
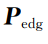
和平面特征点云

传递给回环检测模块。
回环检测模块中进行回环识别和位姿的更新。为实现对井下通道的几何描述,在激光雷达相对坐标系下,进行特征向量提取和中心点计算,基于点云的角度分布和尺度分布关系,构建点云的全局特征描述子;以多维描述子之间的相关性作为点云相似度的评价指标;使用特征点配准方法以改进全局配准计算耗时过大的问题;利用检测到的相似场景建立回环约束,通过因子图优化消除累积误差并保证轨迹和地图的全局一致性。回环检测模块是本文研究的重点,算法流程框图如图1所示。其中:
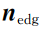
和

分别为边角特征点云和平面特征点云对应的特征向量;

为关键帧

的全局描述子向量;

和

分别为关键帧

的边角特征和平面特征。
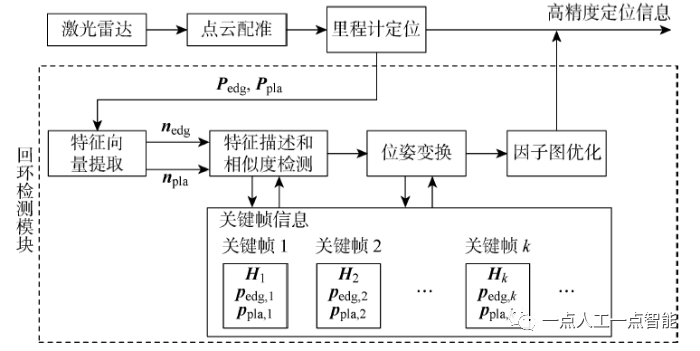
图1 基于全局特征描述子的回环检测算法流程
1.1 特征向量提取
使用全局点云中具有代表性信息的边角特征和平面特征进行数据处理,对里程计模块中提取的边角特征点云

和平面特征点云
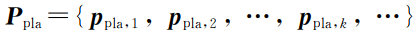
分别提取特征向量。取

或

中的任意一点

,使用

-维(KD)树搜索其所在点云中邻近的

个点,计算该部分点云的协方差矩阵,具体步骤如下。
步骤1 计算邻近
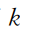
点的质心:

步骤2 计算协方差矩阵

,即质心

到邻近点云中所有点

的向量与其转置的内积:

步骤3 对协方差矩阵进行奇异值分解(SVD),求特征值:

式中:

为矩阵

对应的特征值;为矩阵
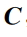
对应的特征向量;

为对角线

组成的对角矩阵;

为奇异值分解后的实正交矩阵。
步骤4 由
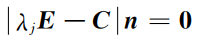
解得对应的特征向量
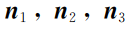
。
其中,边角特征提取线向量为特征向量

,邻近点投影至该方向上的向量方差最最小,为最大特征值

对应的特征向量

;平面特征提取法向量为特征向量

,邻近点投影至该方向上的向量方差最最大,为最小特征值λ1对应的特征向量

[14]。
1.2 特征描述和相似度计算
设计全局特征描述子的计算方法。通过计算全局点云
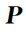
中所有点的三维坐标平均值得到当前帧的点云质心

,以点云

和

中所有点对应的特征向量的均值作为质心

处对应的特征向量

,进而计算点云的全局特征描述子,边角点云
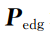
和平面点云

分开计算。
遍历点云
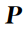
中的所有点,确定以质心
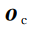
为原点

的参考坐标系
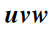
:

式中:

为点云

或

中任意选取的一点;

为点云质心处的归一化特征向量;

为点

到质心

之间的欧氏距离。以

,

确定的坐标系如图2所示,其中:

为点

处归一化之后的特征向量。

图2 全局点云下的uvw坐标系
以上述计算得到的
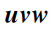
坐标系为基准,计算点云特征向量相对于基准坐标系3个坐标轴的角度分布,则有:

式中:

为点

,

之间的欧氏距离;

为特征向量
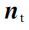
与坐标轴v之间的夹角,值域为[-1,1];
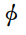
为
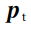
,

之间连线方向与坐标轴

之间的夹角,值域为[-1,1];

为特征向量

投影至

平面时与坐标轴

之间的夹角,值域为[−π/2,π/2]。
利用上述公式进行计算后,

,

,

,

为非线性相关的,可以替代两点的(x,y,z,
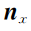
,

,

)共12维数据对点云的分布进行几何关系描述。
遍历点云

和

中所有点,与质心点

构成点对,计算对应的

,

,

,d四要素。将
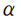
,

,

的值域区间进行等分,统计全局点云三要素在各区间内的分布情况,构成特征描述子的角度分量。
计算全局点云

中距离质心点
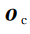
最远的位置,将最大距离均分为多个区间,统计各个点相对于质心距离在区间中的分布,以此构成特征描述子的尺度分量。
最终设计的点云全局描述特征描述子为230维向量,其中前105维为边角特征点云
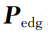
计算得到的角度分量
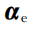
,

,

,中间105维数据为平面特征点云
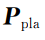
计算得到的角度分量

,

,

,均以35维的向量表示,最后20维数据为当前帧点云
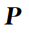
全部点的尺度分量

。
本文提出的全局描述子计算方法以点云中心建立相对坐标系进行计算,具有旋转不变性和平移不变性,如图3所示。图3(a)为原始点云

及其旋转45°、平移10 m后的点云,经旋转和平移变换后,如图3(b)和3(c)所示,点云的全局特征描述子不发生变化。其中:

为描述子

的维度信息;
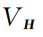
为对应维度的数值信息。旋转不变性和平移不变性说明,对于同一场景下,激光雷达传感器处于不同角度和位置时,仍能进行准确地进行回环检测。

图3 旋转和平移不变性实验
使用点云全局特征描述子的皮尔逊相关系数[15]作为衡量点云相似度的标准,其计算公式如下:

式中:
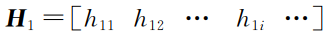
,

为归一化后的点云全局特征描述子;
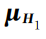
和

分别为

和

元素的平均值向量;

为数学期望;

为方差;

为相关系数,其取值范围为[0, 1]。当
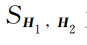
接近于1时,说明特征描述子为正相关关系,点云的相似度越高[16]。
1.3 位姿变换
对筛选后相似度大于阈值的当前帧点云

和历史相似帧点云

进行相对位姿变换的计算。相对位姿的计算使用点云的边角特征和平面特征配准方法,即使用三维点的曲率计算公式[13]计算点云不同位置处的光滑度,以光滑度为依据提取点云的边角特征和平面特征,只对边角特征和平面特征进行点云配准,提高了计算速度。
为减少点云的误匹配概率,使用曲率估计方法对点云配准效果进行验证。当前帧边角点和平面点分别在相似帧边角特征和平面特征中搜索匹配点,对相似帧的特征进行主成分分析,计算其特征值

。
其中,当点云为边角特征时,扫描点按照线方向分布;为平面特征时,扫描点呈现平面式分布,在垂直平面方向上的方差最小。边角特征和平面特征应分别满足如下关系式:

对于配准后的相似帧点云,构建需要求解的目标函数,使用Levenberg-Marquardt法迭代求解使目标函数最小的位姿变换,其目标函数如下:

式中:上标L和W分别为局部和世界坐标系;上划线-为测量值,~为估计值;

为当前边角特征点云

中一点

在激光雷达局部坐标系下的坐标;
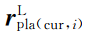
为当前平面特征点云

中一点

在激光雷达局部坐标系下的坐标;

,
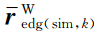
分别为相似帧边角特征点云在世界坐标系下距离
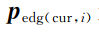
最近的两点坐标;

,

,

分别为相似帧平面特征在世界坐标系下距离

最近的三点坐标;

,
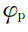
分别为边角和平面特征的目标函数,其含义为配准点到线或平面的距离;
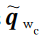
和

为待求解变量,分别为当前坐标系到世界坐标系下的旋转四元数估计值和平移向量估计值。
边角特征和平面特征的配准如图4所示,其中:黑色点云为当前帧;绿色点云为历史相似帧;黑色加粗点为当前帧边角特征点坐标
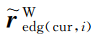
和平面特征点坐标
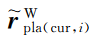
;绿色加粗点分别为相似帧的边角特征点

,

构成直线,以及平面特征点
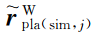
,
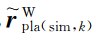
,

构成平面。
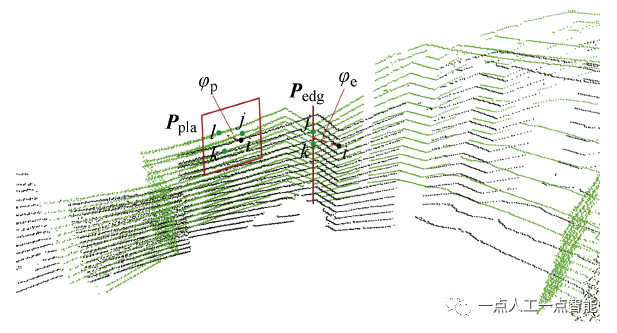
图4 边角特征和平面特征点云配准
1.4 因子图优化
通过位姿变换方法可以获得当前关键帧与历史相似帧之间的相对位姿变换,以此建立新的回环约束,构建因子图如图5所示。其中:

为测量函数;
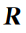
为测量噪声协方差矩阵;因子图由一系列不同时刻位姿测量值

和地图路标点

的观测量构成。每条实线为1次前后帧之间的位姿累积测量事件,每条虚线为1次检测到的回环约束测量事件,将因子图表达转换为线性化的约束的线性矩阵
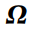
的形式,每一个新的测量值都会致使信息矩阵发生更新。

图5 因子图优化模型
对于1次测量事件,

和

时刻位姿测量值分别为

,

,对应的路标点集合为
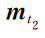
测量事件构成的约束函数如下:
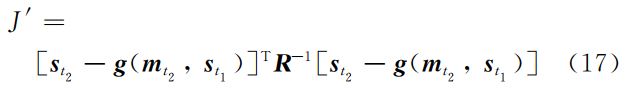
因子图优化的过程为求解目标函数得到概率最大的地图和位姿信息路径,其目标函数为测量约束的集合,目标函数公式如下:
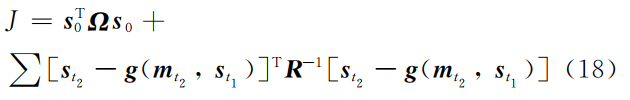
因子图优化的方法将图映射为信息矩阵的表达方式进行求解,利用图的稀疏性特点,在求解过程中保持较低的计算量和错误的数据关联,优于一般的滤波方法[17]。
02 实验结果与讨论
2.1 准确率和召回率实验
准确率和召回率是衡量回环检测模块中相似度检测算法性能的重要指标,在回环检测算法设计中需首先保证较高的准确率,其次在满足高准确率的同时尽可能提高相似度检测模块的召回率。
准确率和召回率的计算方法如下:

式中:
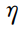
为准确率;

为召回率;TP为正确识别出同一场景的数量;FP为将不同场景错误识别为同一场景的数量;FN为同一场景被错误识别为不同场景的数量。
实验采用苏黎世联邦理工学院公开数据集[18]进行测试,该数据集为手持激光雷达在真实矿井中扫描得到的数据。改变相似度检测算法的阈值ω(0<ω<1),以此测试算法在不同阈值情况下的准确率和召回率,结果如图6所示。
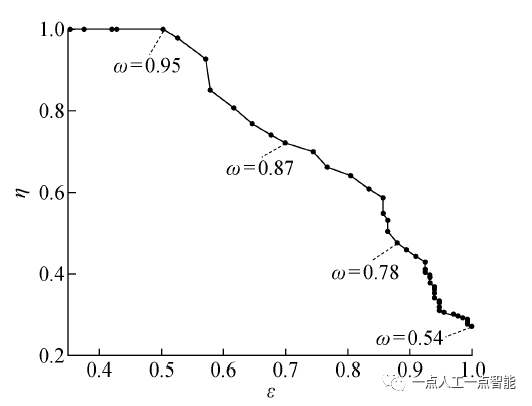
图6 准确率和召回率曲线
由图6可知,在保证准确率为100%的条件下,召回率最高可以达到50。76%,超过一半的相似场景会被召回,此时阈值

为0。95,随着阈值
进一步降低,召回率增大,准确率降低,回环检测可能出现错误匹配,得到错误的位姿信息,对定位和建图产生严重的影响、因此应保证高准确率,在后续算法实验中均将阈值
设置为0。95,此时准确率为100%。
2.2 定位精度实验
本文进行了多组仿真和开源数据集下的定位精度实验。实验平台CPU为AMD 3600,内存16 GB,算法采用C++语言编写,均在Ubuntu 18.0的机器人操作系统(ROS)进行测试。仿真实验中,使用文献[19]提供的开源数据进行测试,该数据来自于美国国防部高级研究计划局(DARPA)在匹斯堡举行的“DARPA地下煤矿挑战赛”。使用该数据集进行了4组实验,其中Sim_mine_1和Sim_mine_2为仿真实验,将井下三维模型导入Gazebo仿真系统,添加传感器进行数据采集,模拟巡检工作。搭建的仿真实验环境如图7所示,仿真实验中以无人机作为载体,上方搭载Velodyne-16激光雷达进行数据采集。

图7 井下仿真实验环境
M100_Underground和M100_Tunnel分别为在真实矿井中大疆M100无人机搭载激光雷达在井下巷道和矿山隧道巡检时录制的数据包文件,其中包含了雷达运动过程中的里程计信息。共进行了4组井下环境的实验,实验中每次巡检结束时,传感器回到起点附近。实验对照算法分别为LOAM[13],以及复现文献[9]的回环检测算法,以LOAM作为前端里程计,使用近邻点搜索和ICP配准进行位姿变换计算的LOAM+ICP算法。将3种定位算法结果分别与仿真实验中记录的真实值或开源数据集中记录的里程计值进行对比。
实验的4个场景分别使用轨迹真实值进行建图,地图情况如图8所示。图8(a)和8(b)分别为仿真环境的地图,为开采矿井的巷道场景,路段分叉多,通道为非结构化场景,缺乏明显特征;图8(c)和8(d)为M100无人机搭载激光雷达扫描得到的地图,图8(c)环境与图8(a)和8(b)类似,分叉路段多,通道为挖掘面,而图8(d)为矿井入口隧道,采用水泥浇筑,具有支撑柱等结构化特征。
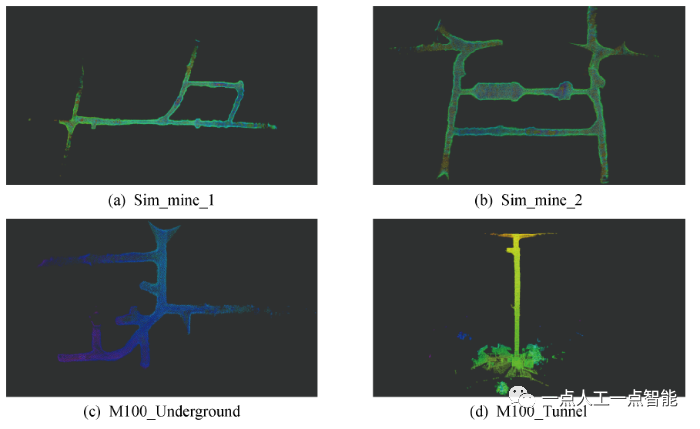
图8 实验场景点云地图
算法定位精度实验中,进行初始坐标系对齐,以均方根误差,全局最大误差值以及终点处的绝对误差作为评价定位精度的指标,实验结果如表1所示,其中:序号1,2,3,4分别为实验Sim_mine_1、实验Sim_mine_2、实验M100_Underground和实验M100_Tunnel。
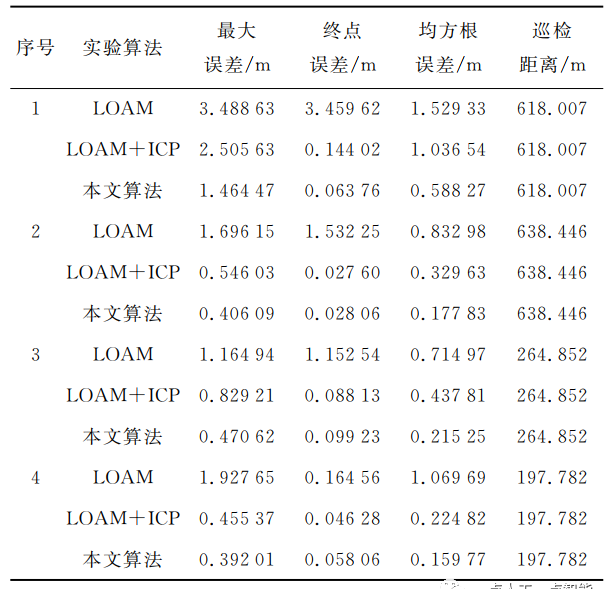
表1 定位精度实验结果
4次实验中,与没有回环检测模块的LOAM算法相比,LOAM+ICP算法和本文算法在最大误差,终点绝对误差以及均方根绝对误差3个指标上均得到明显提高。没有回环检测模块的定位算法随运行时间增长,累积误差逐步增大,体现为LOAM算法的终点绝对误差明显大于其他两种算法,这是造成LOAM算法全局轨迹的均方根误差较大的主要原因。
使用定位评价和可视化工具(EVO)集绘制 Sim_mine_1实验中的定位轨迹,初始坐标轴x,y,z对齐后的轨迹曲线如图9所示,其中:t为时间。3种算法在z坐标下的差值明显,LOAM算法没有回环检测模块,累积误差未得到校正,最终偏移误差绝对值最大;LOAM+ICP和本文算法在加入回环检测后,在巡检轨迹中间段产生一定偏移,但通过回环检测校正了累积误差,全局轨迹的均方根误差较小。

图9 Sim_mine_1定位实验轨迹
与LOAM+ICP算法相比,本文算法的定位精度更高,均方根误差较小,但两者终点绝对误差较为接近。其原因在于LOAM+ICP算法计算速度慢,影响了里程计算法的精度,中期误差大,但当检测到回环时仍能计算出准确的位姿,消除累积误差。实验中LOAM+ICP算法和本文算法回环检测部分各模块的计算耗时如表2所示。
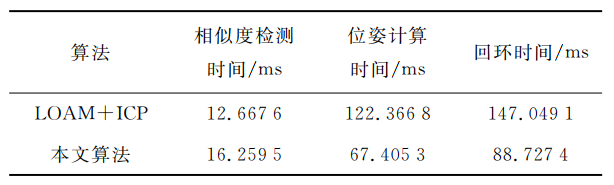
表2 算法各模块运行时间
上述实验数据均为实验过程中记录的单次完整执行对应模块需要的平均耗时。实验结果显示,相似度检测模块中,LOAM+ICP基于位置进行判断,而本文算法需要计算点云描述子,算法步骤较多,在该模块中耗时增加3.5919 ms;而在位姿计算模块,LOAM+ICP通过ICP方法计算相似帧之间的位姿变换,对点云中的所有点进行配准、目标函数的构建和迭代求解,而本文算法基于曲率计算方法,仅对边角和平面特征进行处理和计算,优化了计算效率,平均耗时由 122.3668 ms降至 67.4053 ms,降低了44.92%;回环时间反映了完整执行一次回环检测模块需要的平均时间,得益于位姿计算时间的明显下降,回环检测模块的整体耗时由 147.0491 ms降低为 88.7274 ms。
在LOAM+ICP算法中由于回环检测模块平均耗时超过100 ms,低于点云数据采集频率10 Hz。且基于全局描述子的回环检测方法解决了 LOAM+ICP算法召回率随累积误差增大不断减小的问题,在长时间运行中更加具有优势。
因子图优化模块对于保证轨迹的全局一致性和平滑性有重要作用。Sim_mine_1实验使用本文算法进行因子图优化前后的轨迹如图10所示。其中:绿色轨迹为因子图优化前轨迹;红色轨迹为因子图优化后轨迹。由局部放大图可以看出,优化后点云地图无重影,全局一致性良好,因子图优化前轨迹的均方根误差为 0。888733 m,大于优化后的 0。588270 m。

图10 因子图优化前后轨迹
03 结语
针对井下巡检时定位误差随时间不断累积的问题,提出一种适用于激光SLAM的基于点云全局特征描述子的回环检测方法。该方法具有以下优势:
①充分利用了井下巷道的结构特征,相似度检测不受位姿信息约束,通过曲率分别提取通道四周墙壁边角处和平面处的特征向量,利用特征向量和点云中心点之间的角度关系和点云通道和中心点之间的距离关系构建了全局特征描述子;
②提高了计算速度,基于边角点和平面点配准策略,进行高效率的位姿变换算法研究;
③全局一致性优,采用因子图优化获得了使全局误差最小的位姿,校正了累积误差。
实验结果表明,本文算法定位精度相较于不加回环检测的LOAM算法和使用距离信息进行回环检测的LOAM+ICP算法得到较大提升,在长时间长距离的实验中提升效果显著。实验结果对于井下执行长时间的巡检任务具有指导意义,未来工作中考虑进一步研究,将算法应用于井下巡检无人机平台上,探究在实际应用场景中的可行性。