【计算机视觉】二、图像形成：2、几何基元和几何变换：2D变换

一、向量和矩阵的基本运算

【计算机视觉】二、图像形成：1、向量和矩阵的基本运算：线性变换与齐次坐标

二、几何基元和变换

1、几何基元(Geometric Primitives)

几何基元是计算机图形学中最基本的图形对象,它们是构建更复杂图形的基础单元。常见的几何基元包括:

点(Point): 由一对或一组坐标值表示的零维对象。
线段(Line Segment): 由两个端点确定的一维对象。
多边形(Polygon): 由一系列顶点连接而成的闭合平面图形,是二维对象。
曲线(Curve): 由一系列控制点和方程确定的平滑曲线,如贝塞尔曲线、样条曲线等。
圆(Circle): 由一个圆心和半径确定的二维闭合曲线。
球体(Sphere): 由一个球心和半径确定的三维闭合曲面。

这些基本的几何基元可以通过组合、变换等操作构建出更加复杂的图形对象,如三维模型、场景等。

2、几何变换(Geometric Transformations)

几何变换是针对几何基元进行的一系列操作,用于改变其位置、大小、形状或其他属性。常见的几何变换包括:

平移变换(Translation): 沿着一个向量移动对象的位置。
旋转变换(Rotation): 围绕一个点或轴旋转对象。
缩放变换(Scaling): 改变对象的大小,可以是统一缩放或按不同比例缩放。
剪切变换(Shearing): 沿着一个方向倾斜对象。
反射变换(Reflection): 沿着一条线或一个平面对称地反射对象。

上述变换可以分为 刚体变换 (如平移和旋转)和 非刚体变换 (如缩放、剪切和反射)。刚体变换不改变对象的形状和大小,只改变其位置和方向。非刚体变换会改变对象的形状或大小。此外,还有一些更复杂的变换:

欧几里得变换=刚体变换=等距变换
相似变换(Similarity Transformation): 包括欧几里得变换和等比例缩放。
仿射变换(Affine Transformation): 包括相似变换、缩放、反射和剪切。
射影变换(Projective Transformation): 也称透视变换,可以将三维物体投影到二维平面上。

几何变换通常使用矩阵表示,对点或向量进行矩阵乘法即可完成变换操作。不同的变换对应不同的变换矩阵。

1. 各种变换的关系

使用文氏图(Venn diagram)的形式展示二维变换之间的关系和包含情况：

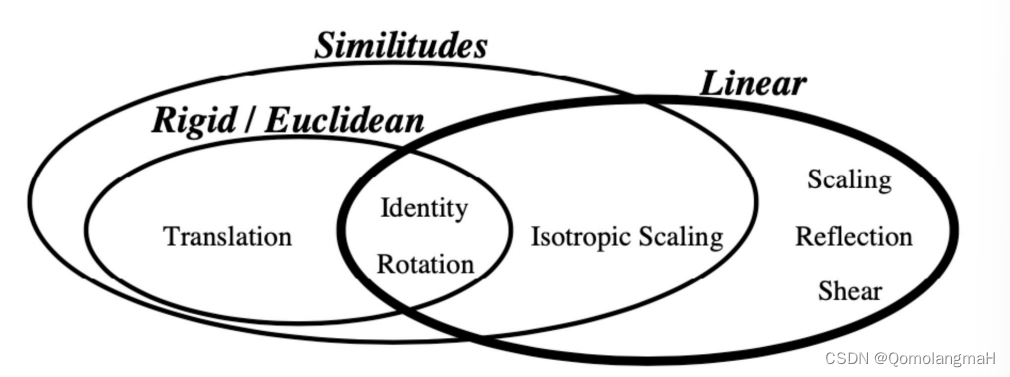
最内层圆圈表示恒等变换(Identity)和旋转变换(Rotation)。
包围它的第二层椭圆表示刚体变换(Rigid/Euclidean),它包含了平移(Translation)和旋转变换。
第三层椭圆表示相似变换(Similitudes),除了包含刚体变换之外,还包含等比例缩放(Isotropic Scaling)。
- 相似变换只包含等比例缩放而没有一般的缩放。
最后一个椭圆表示线性变换(Linear),它包括缩放(Scaling)、反射(Reflection)和错切(Shear)等一般线性变换。

2. 变换公式

平移变换

代码语言：txt

复制

- 二维平移:

x' = \begin{bmatrix}I & t\end{bmatrix}x

代码语言：txt

复制

- 或:

x' = \begin{bmatrix}I & t\\0^T & 1\end{bmatrix}x

欧式变换(旋转+平移)

代码语言：txt

复制

- 二维欧式:

x' = \begin{bmatrix}R & t\end{bmatrix}x

其中R是2x2旋转矩阵:

R = \begin{bmatrix}\cos\theta & -\sin\theta\\\sin\theta & \cos\theta\end{bmatrix}

相似变换(缩放+旋转+平移)

代码语言：txt

复制

- 二维相似:

x' = \begin{bmatrix}sR & t\end{bmatrix}x

其中s为等比例缩放因子,R为旋转矩阵

仿射变换

代码语言：txt

复制

- 二维仿射:

x' = \begin{bmatrix}a_{00} & a_{01} & a_{02}\\a_{10} & a_{11} & a_{12}\end{bmatrix}x

射影变换

代码语言：txt

复制

- 二维射影:

x' = Hx,\ H\ \text{为任意3x3矩阵}

这些变换矩阵提供了将点或向量从一个坐标空间变换到另一个坐标空间的数学表示方法,是计算机图形学、计算机视觉等领域的基础工具。通过设计合适的变换矩阵,可以实现各种几何变换,例如平移、旋转、缩放、透视投影等。

不同类型的变换矩阵在形式和自由度上有所区别,平移矩阵比较简单,相似变换增加了缩放,仿射变换支持非等比缩放和错切,而射影变换是最通用的。矩阵的秩决定了变换的自由度和约束条件。

3. 2D变换的层次

自由度越高,变换的灵活性就越大,但保留的不变性也就越少。最右侧的图标展示了了这些变换所保留的不变性:平移保留方向、刚体保留长度、相似保留角度、仿射保留平行线、射影只保留直线不变。

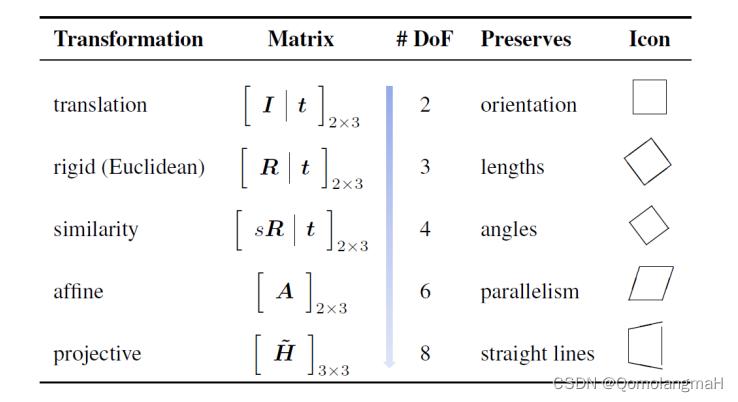
平移变换(translation) 矩阵形式:

\begin{bmatrix}I & t\end{bmatrix}_{2\times 3}

自由度: 2 (对应x,y平移分量)

保留不变性: 方向(orientation)

刚体变换(rigid/Euclidean) 矩阵形式:

\begin{bmatrix}R & t\end{bmatrix}_{2\times 3}

自由度: 3 (1个旋转分量+2个平移分量)

保留不变性: 长度(lengths)

相似变换(similarity) 矩阵形式:

\begin{bmatrix}sR & t\end{bmatrix}_{2\times 3}

自由度: 4 (1个旋转分量+1个缩放分量+2个平移分量)

保留不变性: 角度(angles)

仿射变换(affine) 矩阵形式:

\begin{bmatrix}A\end{bmatrix}_{2\times 3}

自由度: 6 (组合缩放、错切、旋转、平移)

保留不变性: 平行线(parallelism)

射影变换(projective) 矩阵形式:

\begin{bmatrix}H\end{bmatrix}_{3\times 3}

自由度: 8

保留不变性: 直线(straight lines)

4. python实现

代码语言：javascript

复制

import numpy as np
1. 平移变换
def translation(tx, ty):

T = np.array([[1, 0, tx],

[0, 1, ty],

[0, 0, 1]])

return T
2. 欧式变换(旋转+平移)
def rigid_transform(theta, tx, ty):

T = np.array([[np.cos(theta), -np.sin(theta), tx],

[np.sin(theta), np.cos(theta), ty],

[0, 0, 1]])

return T
3. 相似变换(缩放+旋转+平移)
def similarity_transform(s, theta, tx, ty):

T = np.array([[s * np.cos(theta), -s * np.sin(theta), tx],

[s * np.sin(theta), s * np.cos(theta), ty],

[0, 0, 1]])

return T
4. 仿射变换
def affine_transform(a00, a01, a02, a10, a11, a12):

T = np.array([[a00, a01, a02],

[a10, a11, a12],

[0, 0, 1]])

return T
5. 射影变换
def projective_transform(H):

return H
使用示例
points = np.array([[1, 2], [3, 4], [5, 6]])
平移变换
T = translation(10, 20)

new_points = np.hstack([points, np.ones((3, 1))]).dot(T.T)[:, :2]

print(new_points)
欧式变换
R = rigid_transform(np.pi / 4, 10, 20)

new_points = np.hstack([points, np.ones((3, 1))]).dot(R.T)[:, :2]

print(new_points)
相似变换
S = similarity_transform(0.5, np.pi / 3, 10, 20)

new_points = np.hstack([points, np.ones((3, 1))]).dot(S.T)[:, :2]

print(new_points)
仿射变换
A = affine_transform(1, 0.5, 10, 0, 1, 20)

new_points = np.hstack([points, np.ones((3, 1))]).dot(A.T)[:, :2]

print(new_points)